In the following examples, the pSpline variable stores a pointer to the spline object.
Spline type
The property defines whether the spline method is set to "by fit points" or to "by control points". If the value is set to "by fit points," the spline is drawn based on fit points. If the value is set to "by control points," the spline recalculates fit points.
To check the type of spline, use the type() method which returns the spline type as one value from the OdDbSpline::SplineType enumeration:
enum SplineType {
kFitPoints = 0,
kControlPoints = 1
};
For example:
OdString about;
switch(pSpline->type())
{
case OdDbSpline::kControlPoints: about = L"'by control points'"; break;
case OdDbSpline::kFitPoints: about = L"'by fit points'"; break;
}
odPrintConsoleString(L"\nSpline type is %s", about.c_str());
To set a new spline type, use the setType() method, which requires one value from the OdDbSpline::SplineType enumeration (see above). For example:
// Set type to "by fit points"
pSpline->setType(OdDbSpline::kFitPoints);
// Set type to "by control points"
pSpline->setType(OdDbSpline::kControlPoints);
Closed status
The property is a boolean value that defines whether the spline is closed. If the value is "true", the spline is closed and the last point has the same coordinates as the first point. If the value is "false", the spline is open and the last point has different coordinates from the first point.
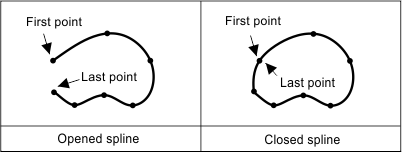
To check the closed status for a spline, use the isClosed() method which returns the status as a boolean value. For example:
odPrintConsoleString(L"\nSpline is %s", ((pSpline->isClosed()) ? L"closed" : L"opened"));
Periodic status
The property is a boolean value that defines whether the spline is periodic. A periodic curve is also a closed spline, but it has two unseen spans at the end of the curve that overlap the first two spans. If the value is "true", the spline is periodic. If the value is "false", the spline is aperiodic.
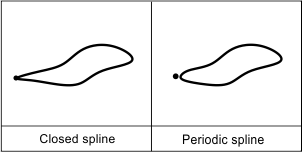
To check the periodic status for a spline, use the isPeriodic() method which returns the status as a boolean value. For example:
odPrintConsoleString(L"\nSpline is %s", ((pSpline->isPeriodic()) ? L"periodic" : L"aperiodic"));
Plane
The spline entity is planar when all of its points lie in the same plane.
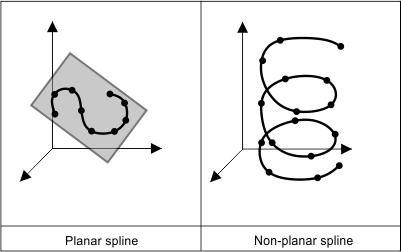
To check whether or not the spline is planar, use the isPlanar() method, which returns a "true" value if the spline object is planar or a "false" value if the spline object is non-planar. For example:
odPrintConsoleString(L"\nSpline is %s", ((pSpline->isPlanar()) ? L"planar" : L"non-planar"));
To get the plane for a spline, use the getPlane() method which requires a reference to a variable of the OdGePlane type in which the plane instance must be saved as the first argument, a reference to a variable of the OdDb::Planarity type in which the plane type must be saved as the second argument, and returns the plane properties through arguments and the resulting code. For example:
OdResult eRes;
OdGePlane plane3d;
double a, b, c, d;
OdDb::Planarity planarity;
eRes = pSpline->getPlane(plane3d, planarity);
if(eRes == eOk && planarity != OdDb::kNonPlanar)
{
plane3d.getCoefficients(a, b, c, d);
odPrintConsoleString(L"\nSpline plane is (%g * X + %g * Y + %g * Z + %g)", a, b, c, d);
}
Spline degree
The order defines the number of nearby control points that influence any given point on the curve. The curve is represented mathematically as a polynomial relation with the degree that is the order minus one (-1). A second-order curve is called a linear spline, a third-order curve is called a quadratic spline, and a fourth-order curve is called a cubic spline. The number of control points must be greater than or equal to the order. Minimum value of spline degree is 1; maximum degree is 25.
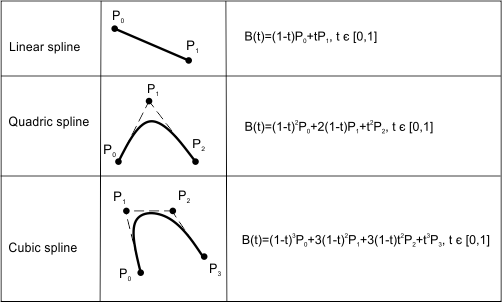
To get the spline degree, use the degree() method, which requires no parameters and returns the spline degree as an integer value. For example:
odPrintConsoleString(L"\nSpline degree is %d", pSpline->degree());
Users can only elevate an existing degree. To do so, use the elevateDegree() method, which requires one integer parameter as a new degree value. For example:
pSpline->elevateDegree(4);
Spline rationality
Splines can be either rational or nonrational. If a spline is rational, each control point has a weight value that influences the curve of the spine near the control point.
To check the spline rationality, use the isRational() method, which returns "true" if the spline is rational or "false" if it is nonrational. For example:
odPrintConsoleString(L"\nSpline is %s", ((pSpline->isRational()) ? L"rational" : L"nonrational"));
Transforming to and converting from an identical 3D GeCurve
A spline entity can be transformed into a 3D GeCurve or converted from a 3D GeCurve that is geometrically identical to the spline curve.
To transform a spline into a 3D curve, use the getOdGeCurve() method, which requires a reference to a pointer of an instance of the OdGeCurve3d type as the first argument in which an identical 3D curve must be saved, a reference to an instance of the OdGeTol type as the second optional argument which specifies an admissible tolerance for transforming, and returns eOk if the result is successful.
For example:
OdGeCurve3d *pCurve3d;
pSpline->getOdGeCurve(pCurve3d);
To convert from a 3D curve, use the setFromOdGeCurve() method, which requires a reference to an existing instance of the stored curve geometry of the OdGeCurve3d type as the first argument from which an identical 3D curve must be loaded, a pointer to the normal of the OdGeVector3d type as the second optional argument, a reference to an instance of the OdGeTol type as the third optional argument which specifies an admissible tolerance for converting, and returns eOk if the result is successful.
For example:
OdGeCurve3d *pCurve3d;
pSpline->getOdGeCurve(pCurve3d);
pSpline->setFromOdGeCurve(*pCurve3d);
Note: If the normal vector is supplied, then it must be perpendicular to the 3D curve being loaded, and this vector becomes the normal of the output curve. If the normal vector is not supplied (NULL), the setFromOdGeCurve() method computes the normal vector itself.
See Also
Computed Properties of splines
Example of Working with Splines
Copyright © 2002 – 2021. Open Design Alliance. All rights reserved.
|