The spline curve is defined by a set of control points, which specify the placement and shape of the spline curve and are three-dimensional points in WCS. NURBS data includes:
- Set of control points — Defines the three-dimensional points in WCS that specify the placement of the spline and adjust the shape of the curve. Control points are indexed beginning at a zero.
- Weights of control points — Improves spline approximation and controls the shape of the curve near the control point.
- Knot vector — Defines a sequence of parameter values that determines where and how the control points affect the spline curve.
- Tolerance — Defines the maximum length on which two control points are considered to be identical.
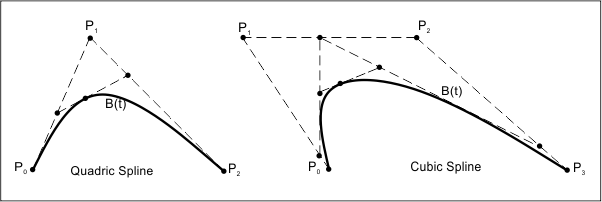
The degree also influences the number of control points. Control points are indexed beginning at zero. Tangent lines construct the curve and define each point B(t) on it subject to the parameter. The quadratic curve starts at P0 to P2, and P1 provides directional information. The cubic curve starts at P0 going toward P1 and arrives at P3 coming from the direction of P2. Usually, it will not pass through P1 or P2, which only provide directional information. The distance between P0 and P1 determines "how far" the curve moves in direction P2 before turning towards P3.
Number of control points
To get the number of spline control points, use the numControlPoints() method, which returns the number of control points as an integer value. For example:
odPrintConsoleString(L"\nSpline has %d control points", pSpline->numControlPoints());
Getting control point data
To get data of each control point, use the getControlPointAt() method, which requires two parameters: an integer value for specifying the index of the control point and a reference to an OdGePoint3d object through which the point data will be returned. For example:
for (int i = 0; i < pSpline->numControlPoints(); i++)
{
OdGePoint3d controlPoint;
pSpline->getControlPointAt(i,controlPoint);
odPrintConsoleString(L"\nControl point %d coordinates: %f %f %f", i, controlPoint.x, controlPoint.y, controlPoint.z);
}
Changing control point data
To change an existing control point, use the setControlPointAt() method, which requires two parameters: an integer value for specifying the index of the existing control point and a reference to an OdGePoint3d object where the new control point data is stored. For example:
OdGePoint3d controlPoint;
// Get the existing control point
pSpline->getControlPointAt(3,controlPoint);
// Change point data
controlPoint.x += 10;
controlPoint.y += 5;
controlPoint.z += 20;
// Set new data to the spline
pSpline->setControlPointAt(3,controlPoint);
Adding new control point
To add a new control point into the spline, use the insertControlPointAt() method, which requires three parameters: a double value to specify the knot parameter at the new point where it should be added, a reference to an OdGePoint3d object as a new control point, and a double value as an optional value of point weight. For example:
// Knot parameter
double knorParam = 50;
pSpline->insertControlPointAt(knorParam, OdGePoint3d(20.0,10.0, 0.0));
Note: Knot parameter should take its value from the range of parameter values.
Removing the existing control point
To remove the existing control point, use the removeControlPointAt() method, which requires one integer parameter for the control point index. The method returns eOk if removal was successful or an error code if it was not. For example:
pSpline->removeControlPointAt(4);
Weight of a control point
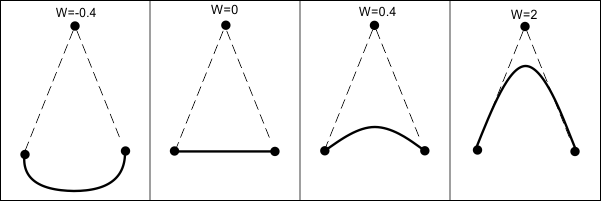
A spline can have an adjustable weight for each control point, which improves spline approximation and controls the shape of the curve near the control point. The closer the weight value is to zero, the closer the curve is to a straight line near the corresponding control point. If the weight increases, the curve pulls toward the corresponding control point. If the weight decreases, the curve pushes from the corresponding control point. A spline is called rational when it has weighted control points.
To get the weight of a control point, use the weightAt() method, which requires one integer parameter to specify the index of a control point and returns the point weight as a double value. For example:
for (int i = 0; i < pSpline->numControlPoints(); i++)
{
odPrintConsoleString(L"\nWeight on %d point is %f", i, pSpline->weightAt(i));
}
To set a new weight to a control point, use the setWeightAt() method, which requires two parameters: an integer value to specify the index of a control point and a double value as the new weight. For example:
for (int i = 0; i < pSpline->numControlPoints(); i++)
{
pSpline->setWeightAt(i, 2.0);
}
Knots
The knot vector is a sequence of parameter values and divides the parametric space into intervals, usually called knot spans. Each time the parameter value enters a new knot span, a new control point becomes active while an old control point is discarded. Therefore, the values in the knot vector should be in ascending order, so (0, 0, 0, 1, 2, 3, 3, 3) is valid, but (0, 0, 2, 0, 3, 1, 3, 3) is invalid.
Consecutive knots can have the same value, defining a knot span of zero length, which implies that two control points are activated at the same time. A number of coinciding knots is sometimes referred to as a knot with a certain multiplicity. Knots with multiplicity two or three are known as double or triple knots. The multiplicity of a knot is limited to the degree of the curve, since a higher multiplicity would split the curve into disjoint parts and leave control points unused. The knot vector usually starts with a knot that has multiplicity equal to the order, since this activates the control points that have influence on the first knot span. Similarly, the knot vector usually ends with a knot of that multiplicity. Curves with such knot vectors start and end in a control point.
The individual knot values are not meaningful by themselves; only the ratios of the difference between the knot values matter. Hence, the knot vectors (0, 0, 1, 2, 3, 3) and (0, 0, 2, 4, 6, 6) produce the same curve. The positions of the knot values influence the mapping of parameter space to curve space.
To get the knots data, use the getNurbsData() method, which returns nine values through the nine parameters: reference to an integer value for the spline degree, reference to a boolean value for the 'spline rational' property, reference to a boolean value for the 'closed' status, reference to a boolean value for the 'periodic' status, reference to an OdGePoint3dArray object for the array of control points, reference to an OdGeDoubleArray object for the array of knots, reference to an OdGeDoubleArray object for the weights of control points, reference to a double value for the control point tolerance, and reference to a double value for the knot tolerance. For example:
int degree;
bool rational;
bool closed;
bool periodic;
OdGePoint3dArray controlPoints;
OdGeDoubleArray knots;
OdGeDoubleArray weights;
double controlPtTol;
double knotTol;
pSpline->getNurbsData(degree, rational, closed, periodic, controlPoints, knots, weights, controlPtTol, knotTol);
for (int i = 0; i < knots.size(); i++)
{
odPrintConsoleString(L"\nKnot %d is %f", i, knots[i]);
}
Getting and setting the NURBS data
To get the NURBS data, use the getNurbsData() method, which returns nine values through nine parameters: reference to an integer value for the spline degree, reference to a boolean value for the 'spline rational' property, reference to a boolean value for the 'closed' status, reference to a boolean value for the 'periodic' status, reference to an OdGePoint3dArray object for the array of control points, reference to an OdGeDoubleArray object for the array of knots, reference to an OdGeDoubleArray object for the weights of control points, reference to a double value for the control point tolerance, and reference to a double value for the knot tolerance.
For example:
// Declare variables
int degree;
bool rational;
bool closed;
bool periodic;
OdGePoint3dArray controlPoints;
OdGeDoubleArray knots;
OdGeDoubleArray weights;
double controlPtTol;
double knotTol;
// Get NURBS data
pSpline->getNurbsData(degree, rational, closed, periodic, controlPoints, knots, weights, controlPtTol, knotTol);
// Display some parameters
for (int i = 0; i < controlPoints.size(); i++)
{
odPrintConsoleString(L"\nControl point %d coordinates: %f %f %f", i, controlPoints[i].x, controlPoints[i].y, controlPoints[i].z);
}
odPrintConsoleString(L"\nControl point tolerance: %f", controlPtTol);
odPrintConsoleString(L"\nSpline is %s", ((periodic) ? L"periodic" : L"aperiodic"));
To set the NURBS data, use the setNurbsData() method, which requires nine values: integer value for the spline degree, boolean value for the 'spline rational' property, boolean value for the 'closed' status, boolean value for the 'periodic' status, reference to an OdGePoint3dArray object for the array of control points, reference to an OdGeDoubleArray object for the array of knots, reference to an OdGeDoubleArray object for the weights of control points, double value for the control point tolerance, and double value for the knot tolerance.
For example:
/* Declare variables */
// Declare degree
int degree = 3;
// Declare 'rational' property
bool rational = false;
// Declare 'closed' status
bool closed = false;
// Declare 'periodic' status
bool periodic = false;
// Declare array of control points
OdGePoint3dArray controlPoints;
controlPoints.setLogicalLength(5);
controlPoints[0] = OdGePoint3d(0.0, 0.0, 0.0);
controlPoints[1] = OdGePoint3d(1.0, 3.0, 0.0);
controlPoints[2] = OdGePoint3d(3.0, 5.0, 0.0);
controlPoints[3] = OdGePoint3d(4.0, 4.0, 0.0);
controlPoints[4] = OdGePoint3d(1.0, 6.0, 0.0);
// Declare array of knots
OdGeDoubleArray knots;
knots.setLogicalLength(9); // (num_points)+(degree)+1 = 3+5+1 = 9
knots[0] = 0.0;
knots[1] = 0.0;
knots[2] = 0.0;
knots[3] = 0.0;
knots[4] = 2.0;
knots[5] = 3.0;
knots[6] = 3.0;
knots[7] = 3.0;
knots[8] = 3.0;
// Declare array of weights
OdGeDoubleArray weights;
// Declare tolerance of control points
double controlPtTol = 0.000001;
// Declare tolerance of the knots
double knotTol = 0.000001;
/* Set NURBS data */
pSpline->setNurbsData(degree, rational, closed, periodic, controlPoints, knots, weights, controlPtTol, knotTol);
See Also
Specific Properties of Splines
Computed Properties of Splines
Example of Working with Splines
Copyright © 2002 – 2021. Open Design Alliance. All rights reserved.
|