Types of Polylines and Vertices

A two-dimensional polyline object can have the following curve types:

Simple polyline — Defines the polyline curve in which all segments are straight lines and arcs. Each segment is defined by data stored at a vertex, which begins the segment.
Curve-fit — Defines the polyline curve in which all segments are circular arcs so that each segment is specified by two vertices and consists of two arcs. The first vertex defines the start point of the segment, the second vertex defines the bend point between the two arcs, and the next vertex defines the end point of the given segment and the start point for the next segment. The number of vertices is two times more than the number of segments, and the segments are specified by coordinates of vertices, bulges of arcs, and optionally may be specified by tangents.
Spline-fit — Defines the polyline curve in which all segments are cubic or quadratic splines, which use the vertices as control points to build their own spline segments.

A three-dimensional polyline object can have only two curve types: simple polyline and spline-fit. It cannot have arcs of the simple polyline curve type.

A polyline object determines the curve shape using the type property. The spline, circular, and linear curves require a different number of vertices and use different determining geometry. To switch between types, the polyline object adds or removes the vertices and recalculates the parameters of segments. You can change the polyline type manually (using the setPolyType() method) and then change all vertices or use special methods to change the polyline type and recalculate properties of each vertex (using the straighten(), curveFit(), and splineFit() methods) or transform the polyline into other type (using the convertToPolyType() method).

Structurally, two-dimensional and three-dimensional polylines are containers that store their own vertices as individual entities and provide access to them using an iterator or ID. Each vertex entity stores the position and properties of segments (type, bulge, tangent, widths) that determine how the next segment will be drawn. The segment type determines whether the vertex is used for storing and specifying the polyline curve in a plane or if it is used for spline or curve fitting of segments.

Working with segments requires finding an existing vertex in a container, and getting and changing the segment properties using the interface of the two-dimensional or three-dimensional vertex object. In the following examples, the p2dPL variable stores a pointer to a two-dimensional polyline object, and the p3dPL variable stores a pointer to a three-dimensional polyline object.

Curve type

Curve type determines the form of a polyline, that is, how it will be drawn and which types of vertices should be used.

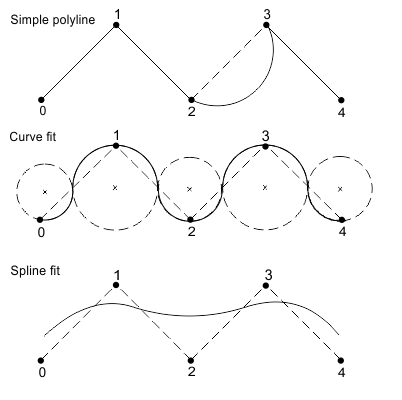
The OdDb::Poly2dType enumeration declares the following types for two-dimensional polylines:


enum Poly2dType {
  k2dSimplePoly = 0, // default
  k2dFitCurvePoly = 1,
  k2dQuadSplinePoly = 2,
  k2dCubicSplinePoly = 3
};

The OdDb::Poly3dType enumeration declares the following types for three-dimensional polylines:


enum Poly3dType {
  k3dSimplePoly = 0, // default
  k3dQuadSplinePoly = 1,
  k3dCubicSplinePoly = 2
};

The types are as follows:

k2dSimplePoly(k3dSimplePoly) — Polyline consists only of Simple type vertices and contains linear and arc segments (no arcs for k3dSimplePoly curve type).
k2dFitCurvePoly — Polyline consists of arc segments passing through Simple type vertices and having extra Curve-fit type vertices between each pair of Simple type vertices to determine an inflection point.
k2dQuadSplinePoly(k3dQuadSplinePoly) — Polyline contains quadratic B-spline segments; Simple type vertices are used as control points to create Spline-fit type vertices, which are needed to form new line segments.
k2dCubicSplinePoly(k3dCubicSplinePoly) — Polyline contains cubic B-spline segments; Simple type vertices are used as control points to create Spline-fit type vertices, which are needed to form new line segments.

To get the polyline curve type, use the polyType() method which returns the curve type as a value of the Poly2dType or Poly3dType enumeration.

For example, a two-dimensional polyline:


OdString about;

switch( p2dPL->polyType() )
{
  case OdDb::k2dSimplePoly:	  about = L"simple 2D polyline";   break;
  case OdDb::k2dFitCurvePoly:	  about = L"2D arc-wavy curve";    break;
  case OdDb::k2dQuadSplinePoly:   about = L"2D quadratic spline";  break;
  case OdDb::k2dCubicSplinePoly:  about = L"2D cubic spline";      break;
}
odPrintConsoleString(L"\n2D Polyline curve type is %s", about.c_str());

For example, a three-dimensional polyline:


switch( p3dPL->polyType() )
{
  case OdDb::k3dSimplePoly:	  about = L"simple 3D polyline";   break;
  case OdDb::k3dQuadSplinePoly:   about = L"3D quadratic spline";  break;
  case OdDb::k3dCubicSplinePoly:  about = L"3D cubic spline";      break;
}
odPrintConsoleString(L"\n3D Polyline curve type is %s", about.c_str());

To set the polyline curve type, use the setPolyType() method which requires the type value of the Poly2dType or Poly3dType enumeration as an argument.

For example, a two-dimensional polyline:


// Set the 2D simple polyline type
p2dPL->setPolyType(OdDb::k2dSimplePoly);

// Set the 2D arc-wavy curve type
p2dPL->setPolyType(OdDb::k2dFitCurvePoly);

// Set the 2D quadratic spline type
p2dPL->setPolyType(OdDb::k2dQuadSplinePoly);

// Set the 2D cubic spline type
p2dPL->setPolyType(OdDb::k2dCubicSplinePoly);

For example, a three-dimensional polyline:


// Set the 3D simple polyline type
p3dPL->setPolyType(OdDb::k3dSimplePoly);

// Set the 3D quadratic spline type
p3dPL->setPolyType(OdDb::k3dQuadSplinePoly);

// Set the 3D cubic spline type
p3dPL->setPolyType(OdDb::k3dCubicSplinePoly);

Note: The setPolyType() method changes only the type value; it does not recalculate the curve shape and does not provide fitting of segments.

Vertex type

Each two-dimensional or three-dimensional vertex object in a polyline stores its type which determines its role in drawing the polyline. Depending on its type, each vertex can be used as a simple vertex for a simple polyline or curve-fit polyline, as a bend point between simple vertices in a curve-fit polyline, or as a control vertex or calculated spline vertex in a spline-fit curve.

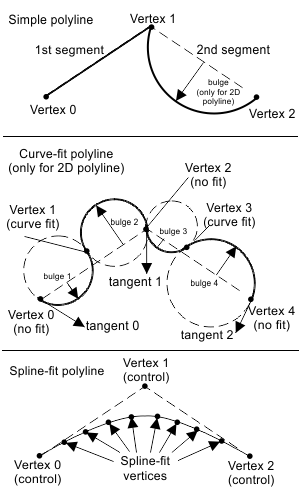
The OdDb::Vertex2dType enumeration declares the following types for two-dimensional vertices:


enum Vertex2dType {
  k2dVertex = 0,          // default,simple non-fit vertex for simple polyline and curve-fit polyline
  k2dSplineCtlVertex = 1, // control vertex for spline-fit polyline
  k2dSplineFitVertex = 2, // spline-fit vertex for approximation in spline-fit polyline
  k2dCurveFitVertex = 3   // curve-fit vertex for approximation in curve-fit polyline
};

The OdDb::Vertex3dType enumeration declares the following types for three-dimensional vertices:


enum Vertex3dType {
  k3dSimpleVertex = 0,  //default, simple non-fit vertex for simple polyline
  k3dControlVertex = 1, // control vertex for spline-fit polyline
  k3dFitVertex = 2      // curve-fit vertex for approximation in curve-fit polyline
};

To get the vertex type, declare an iterator or use its object ID and call the vertexType() method of the obtained vertex which returns the vertex type as one value of the Vertex2dType or Vertex3dType enumeration.

For example, a two-dimensional polyline:


OdInt16 index;
OdString about;

OdDbObjectIteratorPtr itVertex = p2dPL->vertexIterator();

for(itVertex->start(), index = 0 ; !itVertex->done() ; index++, itVertex->step())
{
  OdDb2dVertexPtr pVertex = (OdDb2dVertexPtr)itVertex->entity();
  switch( pVertex->vertexType() )
  {
    case OdDb::k2dVertex:	    about = L"no-fit";      break;
    case OdDb::k2dSplineCtlVertex:  about = L"control";     break;
    case OdDb::k2dSplineFitVertex:  about = L"spline-fit";  break;
    case OdDb::k2dCurveFitVertex:   about = L"curve-fit";   break;
  }
  odPrintConsoleString(L"\n2D Vertex(%d) type is %s", index, about.c_str());
  
}

For example, a three-dimensional polyline:


OdInt16 index;
OdString about;

OdDbObjectIteratorPtr itVertex = p3dPL->vertexIterator();

for(itVertex->start(), index = 0 ; !itVertex->done() ; index++, itVertex->step())
{
  OdDb3dPolylineVertexPtr pVertex;
  pVertex = (OdDb3dPolylineVertexPtr)itVertex->entity();
  switch( pVertex->vertexType() )
  {
    case OdDb::k3dSimpleVertex:	    about = L"no-fit";      break;
    case OdDb::k3dControlVertex:    about = L"control";     break;
    case OdDb::k3dFitVertex:        about = L"spline-fit";  break;
  }
  odPrintConsoleString(L"\n3D Vertex(%d) type is %s", index, about.c_str());
}

To set the vertex type, get the vertex object using an iterator or object ID and use the setVertexType() method of the obtained vertex which requires the type value of the Vertex2dType enumeration as an argument.

For example, a two-dimensional polyline:


for(itVertex->start(), index = 1  ; !itVertex->done() ; index++, itVertex->step())
{
  if(index % 2)
    // Set the control vertex type
	p2dPL->openVertex(itVertex->objectId(), OdDb::kForWrite)->setVertexType(k2dVertex);
  else
    // Set the curve-fit vertex type
	p2dPL->openVertex(itVertex->objectId(), OdDb::kForWrite)->setVertexType(k2dCurveFitVertex);
}

For example, a three-dimensional polyline:


for(itVertex->start(), index = 1  ; !itVertex->done() ; index++, itVertex->step())
{
  if(index % 2)
    // Set the control vertex type
	p3dPL->openVertex(itVertex->objectId(), OdDb::kForWrite)->setVertexType(k3dSimpleVertex);
  else
    // Set the curve-fit vertex type
	p3dPL->openVertex(itVertex->objectId(), OdDb::kForWrite)->setVertexType(k3dControlVertex);
}

Note: The setVertexType() method changes only the type value; it does not recalculate the segment properties.

Changing fit type of the polyline curve

There are four methods for transforming a polyline object from one curve type to another:

straighten() method — Transforms the polyline curve to a sequence of straight lines connected in determinative vertices, removes all fit vertices, clears bulges and tangents of segments, and creates the broken line.
curveFit() method — Transforms the polyline curve to a sequence of circular arcs connected in determinative vertices marked as the Simple type and united in pairs so that each segment is represented as two arcs connected through a bend point marked as the Curve-fit type, redoubles the number of vertices, recalculates the bulges and tangents of segments, and creates an arc-wavy curve.
splineFit() method — Transforms the polyline curve to a sequence of spline segments connected through vertices marked as the Spline-fit type, changes the number of vertices subject to the approximation algorithm, stores original coordinates in vertices marked by the Control type, clears bulges and tangents of segments, and creates a spline curve. The curve-fit and spline-fit methods mark the determinative vertices as Control type to have the ability of back-transforming to the original sequence of segments and vertices.
convertToPolyType() method — Transforms the polyline curve to a simple polyline, arc-wavy curve, cubic spline, or quadratic spline using the type value passed as an argument.

To transform the polyline curve, call the straighten(), curveFit(), or splineFit() method.

For example, a two-dimensional polyline:


// Transform to the cubic spline
p2dPL->splineFit();

// Transform to the arc-wavy curve
p2dPL->curveFit();

// Transform to the broken line
p2dPL->straighten();

For example, a three-dimensional polyline:


// Transform to the cubic spline
p3dPL->splineFit();

// Transform to the broken line
p3dPL->straighten();

To transform the polyline to a specified curve, use the convertToPolyType() method which requires one value from the Poly2dType or Poly3dType enumeration as an argument.

For example, a two-dimensional polyline:


// Transform to the cubic spline
p2dPL->convertToPolyType(OdDb::k2dCubicSplinePoly);

// Transform to the quadratic spline
p2dPL->convertToPolyType(OdDb::k2dQuadSplinePoly);

// Transform to the arc-wavy curve
p2dPL->convertToPolyType(OdDb::k2dFitCurvePoly);

// Transform to the simple polyline
p2dPL->convertToPolyType(OdDb::k2dSimplePoly);

For example, a three-dimensional polyline:


// Transform to the cubic spline
p3dPL->convertToPolyType(OdDb::k3dCubicSplinePoly);

// Transform to the quadratic spline
p3dPL->convertToPolyType(OdDb::k3dQuadSplinePoly);

// Transform to the simple polyline
p3dPL->convertToPolyType(OdDb::k3dSimplePoly);

Conversion between OdDbPolyline and OdDb2dPolyline objects

An OdDbPolyline object can be converted to or from an OdDb2dPolyline object. To allow this action, the PLINETYPE system variable must be set to 2. PLINETYPE controls polyline creation and conversion from OdDb2dPolyline to OdDbPolyline and can have the following values:

0 — Conversions disabled; new polylines are OdDb2dPolyline.
1 — Conversions disabled; new polylines are OdDbPolyline.
2 — Conversions enabled; new polylines are OdDbPolyline.

To convert an OdDbPolyline object to an OdDb2dPolyline object, use the convertTo() method of the OdDbPolyline class. It requires two parameters: a pointer to the OdDb2dPolyline object to be converted to and a bool value, which determines whether to do a handOverTo() between this OdDbPolyline entity and the destination OdDb2dPolyline entity.

For example (pPL is a pointer to the OdDbPolyline object):


pPL->convertTo(p2dPL, true);

To convert an OdDb2dPolyline object to an OdDbPolyline object, use the convertTo() method of the OdDbPolyline class. It requires two parameters: a pointer to the OdDb2dPolyline object to be converted to and a bool value, which determines whether to do a handOverTo() between the source OdDb2dPolyline entity and this OdDbPolyline entity.

For example (pPL is a pointer to the OdDbPolyline object):


pPL->convertTo(p2dPL, true);

Curve type

Vertex type

Changing fit type of the polyline curve

Conversion between OdDbPolyline and OdDb2dPolyline objects

See Also