Specific Properties of Polylines

In the following examples, the p2dPL variable stores a pointer to a two-dimensional polyline object, and the p3dPL variable stores a pointer to a three-dimensional polyline object.

Closed status

This property is a boolean value that defines whether the polyline curve is closed. If the value is "true", the polyline is closed and the last vertex is connected with the first vertex. If the value is "false", the polyline is open and the first vertex and last vertex are not connected. The initial value is "false" (open) by default.

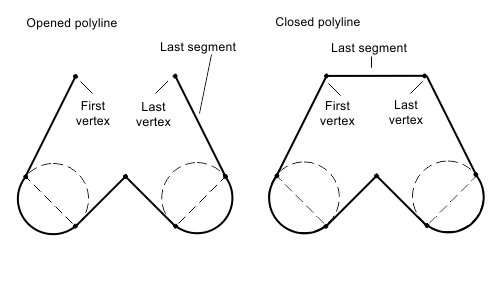
To check the closed status for a two-dimensional or three-dimensional polyline, use the isClosed() method which returns the status as a boolean value. For example:


// 2D-Polyline
odPrintConsoleString(L"\n2D-Polyline is %s", ((p2dPL->isClosed()) ? L"closed" : L"opened"));

//3D-Polyline
odPrintConsoleString(L"\n3D-Polyline is %s", ((p3dPL->isClosed()) ? L"closed" : L"opened"));

To switch the closed status for a two-dimensional or three-dimensional polyline, use the makeClosed() and makeOpen() methods which do not have arguments. For example:


// Make the closed 2D or 3D polyline
p2dPL->makeClosed();
p3dPL->makeClosed();

// Make the opened 2D or 3D polyline
p2dPL->makeOpen();
p3dPL->makeOpen();

Periodic status

This property is a boolean value that defines whether the polyline curve is periodic, that is, whether its segments iterate. If the value is "true", the polyline is periodic. If the value is "false", the polyline is unperiodic. This property is calculated and the initial value depends on the geometry.

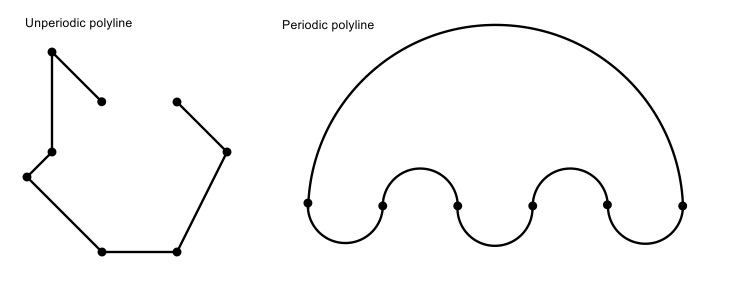
To check the periodic status for a two-dimensional or three-dimensional polyline, use the isPeriodic() method which returns the status as a boolean value. For example:


// 2D-Polyline
odPrintConsoleString(L"\n2D-Polyline is %s", ((p2dPL->isPeriodic()) ? L"periodic" : L"unperiodic"));

//3D-Polyline
odPrintConsoleString(L"\n3D-Polyline is %s", ((p3dPL->isPeriodic()) ? L"periodic" : L"unperiodic"));

Plane

A two-dimensional polyline is a planar entity. The plane is oriented to (0*X + 0*Y + 1*Z + 0) by default. A three-dimensional polyline is planar when all vertices lie in the same plane.

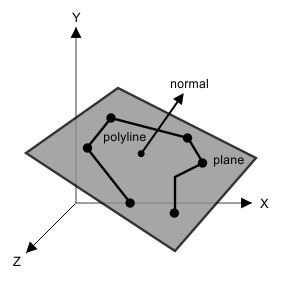
To get the plane for a two-dimensional or three-dimensional polyline, use the getPlane() method which requires a reference to a variable of the OdGePlane type in which the plane instance must be saved as the first argument, a reference to a variable of the OdDb::Planarity type in which the plane type must be saved as the second argument, and returns the plane properties through arguments and resulting code. To check whether a polyline is planar, use the isPlanar() method. For example:


OdResult eRes; 
OdGePlane plane2dPL, plane3dPL;
double a, b, c, d;
OdDb::Planarity planarity;

eRes = p2dPL->getPlane(plane2dPL, planarity);

if(eRes == eOk && planarity != OdDb::kNonPlanar)
{
  plane2dPL.getCoefficients(a, b, c, d);
  odPrintConsoleString(L"2D-Polyline plane is (%g * X + %g * Y + %g * Z + %g)", a, b, c, d);
}

eRes = p3dPL->getPlane(plane3dPL, planarity);

if(eRes == eOk && planarity != OdDb::kNonPlanar)
{
  plane3dPL.getCoefficients(a, b, c, d);
  odPrintConsoleString(L"3D-Polyline plane is (%g * X + %g * Y + %g * Z + %g)", a, b, c, d);
}

Normal

This property defines the normal to the plane in which the two-dimensional polyline is placed. The normal defines the orientation of the polyline in world space. The normal has the coordinates (0,0,1) by default.

To get the normal, use the normal() method which returns the three-dimensional unit vector as an instance of the OdGeVector3d type. For example:


OdGeVector3d normal = p2dPL->normal();
odPrintConsoleString(L"\nNormal = (%g,%g,%g)", normal.x, normal.y, normal.z);

To set the normal, use the setNormal() method which requires the three-dimensional vector as an argument of the OdGeVector3d type and does not return a value. For example:


OdGeVector3d vector(0.303, 0.303, 0.707);
p2dPL->setNormal(vector);

Note: There is no "normal" property for three-dimensional polylines.

Elevation

The property defines the distance from the origin of the world coordinate system to the plane of the two-dimensional polyline entity along the normal named as an elevation. The elevation offsets the polyline plane in world space. The initial value is zero by default.

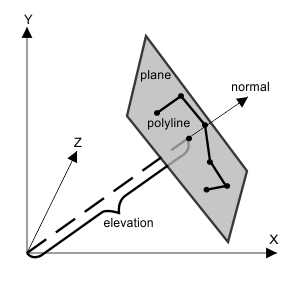
To get an elevation, use the elevation() method which returns the distance to the polyline plane as a double value. For example:


double distance = p2dPL->elevation();

odPrintConsoleString(L"\nElevation = %g", distance);

To set an elevation, use the setElevation() method which requires a distance to the polyline plane as an argument of a double type. For example:


p2dPL->setElevation(2.5);

Note: The ELEVATION system variable stores the default elevation value for new entities, including polylines, created in model space. Also, there is no "elevation" property for three-dimensional polylines.

Thickness

This property is a double value in drawing units that defines a thickness which is the third dimension obtained by offsetting the planar polyline curve along the normal. A positive value defines the thickness to be drawn along the normal direction. A negative value defines the thickness to be drawn in the opposite direction from the normal. A zero value defines a polyline without thickness. The thickness is zero by default.

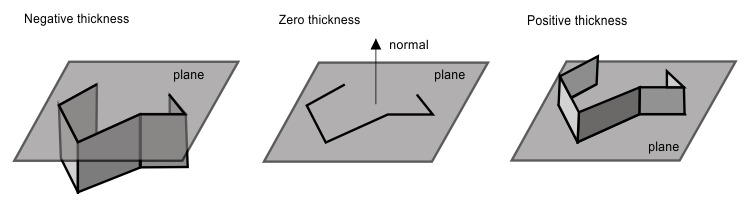
To get a thickness, use the thickness() method which returns the thickness as a double value. For example:


odPrintConsoleString(L"\nPolyline thickness = %g", p2dPL->thickness());

To set a thickness, use the setThickness() method which requires a double value as an argument. For example:


p2dPL->setThickness(1.5);

Note: The THICKNESS system variable stores the default thickness value for new entities, including polylines. Also, there is no "thickness" property for three-dimensional polylines.

Transforming to and converting from an identical 3D curve

A two-dimensional or three-dimensional polyline can be transformed into a 3D curve or converted from a 3D curve that is geometrically identical to the polyline curve.

To transform to a 3D curve, use the getOdGeCurve() method, which requires a reference to a pointer of an instance of the OdGeCurve3d type as the first argument in which an identical 3D curve must be saved, a reference to an instance of the OdGeTol type as the second optional argument which specifies an admissible tolerance for transforming, and returns eOk if the result is successful. For example:


OdGeCurve3d *pCurve2d, *pCurve3d;
//2D-Polyline                
p2dPL->getOdGeCurve(pCurve2d);

// 3D-Polyline
p3dPL->getOdGeCurve(pCurve3d);

To convert from a 3D curve, use the setFromOdGeCurve() method, which requires a reference to an existing instance stored as the curve geometry of the OdGeCurve3d type as the first argument from which an identical 3D curve must be loaded, a pointer to the normal of the OdGeVector3d type as the second optional argument, a reference to an instance of the OdGeTol type as the third optional argument which specifies an admissible tolerance for converting, and returns eOk if the result is successful. For example:


OdGeCurve3d curve2d, curve3d;

//2D-Polyline                 
p2dPL->setFromOdGeCurve(curve2d);

// 3D-Polyline
p3dPL->setFromOdGeCurve(curve3d);

Note: If the normal vector is supplied, it must be perpendicular to the 3D curve being loaded, and this vector becomes the normal of the output curve. If the normal vector is not supplied, that is, NULL, the setFromOdGeCurve() method computes the normal vector itself.

Entity coordinate system matrix

The property defines the transformation matrix that allows converting the two-dimensional polyline geometry between OCS and WCS. The ECS is the entity's coordinate system based on its normal and base point. A two-dimensional polyline takes into account only the normal. The origin is always zero in an ECS matrix. To get the matrix, use the getEcs() method which returns the transformation matrix as an instance of the OdGeMatrix3d type. For example:


OdInt16 row, col;
OdGeMatrix3d matrix;

matrix = p2dPL->getEcs();

odPrintConsoleString(L"\nMatrix:");
for(row = 0 ; row < 4 ; row++)
{
  odPrintConsoleString(L"\n");
  for(col = 0 ; col < 4 ; col++)
    odPrintConsoleString(L"%12g  ", matrix(row, col));
}