The trace object uses four points, the normal, and the thickness to define the geometry to be drawn. In examples, the pTrace variable stores a pointer to the trace object.
Points
The Points property defines four points of the trace in three-dimensional coordinates. Vertices are enumerated as 0, 1, 2, 3. All points are connected by linear segments in the closed figure. The end of the current segment is the start of the next segment and the last segment connects with the first segment. When the coordinates of two points overlap, two adjacent triangles will be drawn. When two points coincide, a triangle will be drawn. All points have the coordinates (0,0,0) by default.
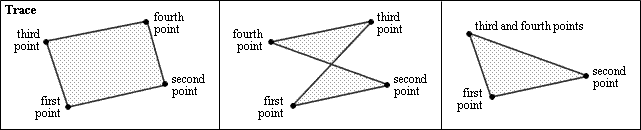
To get the point, use the getPointAt() method which requires a point index in the range 0 to 3 as the first argument of an Integer type, requires a reference to an existing three-dimensional point instance as the second argument of the OdGePoint3d type, and returns the specified point through the second argument. For example:
OdGePoint3d point1, point2, point3, point4;
pTrace->getPointAt(0, point1);
pTrace->getPointAt(1, point2);
pTrace->getPointAt(2, point3);
pTrace->getPointAt(3, point4);
odPrintConsoleString(L"\nPoint1 = (%g,%g,%g)", point1.x, point1.y, point1.z);
odPrintConsoleString(L"\nPoint2 = (%g,%g,%g)", point2.x, point2.y, point2.z);
odPrintConsoleString(L"\nPoint3 = (%g,%g,%g)", point3.x, point3.y, point3.z);
odPrintConsoleString(L"\nPoint4 = (%g,%g,%g)", point4.x, point4.y, point4.z);
To set the point, use the setPointAt() method which requires a point index in range 0 to 3 as the first argument of an Integer type, the three-dimensional point as the second argument of the OdGePoint3d type, and does not return a value. For example:
OdGePoint3d corner1(1, 1, 0);
OdGePoint3d corner2(6, 3, 0);
OdGePoint3d corner3(3, 6, 0);
OdGePoint3d corner4(9, 9, 0);
pTrace->setPointAt(0, corner1);
pTrace->setPointAt(1, corner2);
pTrace->setPointAt(2, corner3);
pTrace->setPointAt(3, corner4);
Normal
The Normal property defines the normal to the plane in which the trace is placed. The normal defines the orientation of the trace plane in world space. The normal has the coordinates (0,0,1) by default.
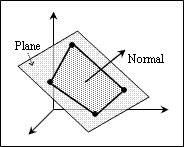
To get the normal, use the normal() method which does not have arguments and returns the three-dimensional vector as an instance of the OdGeVector3d type. For example:
OdGeVector3d normal = pTrace->normal();
odPrintConsoleString(L"\nNormal = (%g,%g,%g)", normal.x, normal.y, normal.z);
To set the normal, use the setNormal() method which requires the three-dimensional vector as an argument of the OdGeVector3d type and does not return a value. For example:
OdGeVector3d vector(0.606, 0.101, 0.303);
pTrace->setNormal(vector);
The setNormal() method automatically converts the specified coordinates to the unit vector. For example:
pTrace->setNormal( OdGeVector3d(2.5, 1.2, 3.4) );
OdGeVector3d result = pTrace->normal();
odPrintConsoleString(L"\n(%g, %g, %g)", result.x, result.y, result.z);
// (0.569803, 0.273505, 0.774932)
Thickness
The Thickness property defines the thickness of the trace as a Double value in drawing units. A positive value defines the thickness to be drawn along the normal direction. A negative value defines the thickness to be drawn in the opposite direction from the normal. A zero value defines a trace without thickness. The thickness is zero by default.
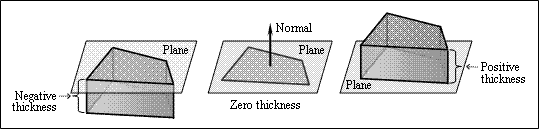
To get the thickness, use the thickness() method which does not have arguments and returns the thickness as a Double value. For example:
odPrintConsoleString(L"\nThickness = %g", pTrace->thickness());
To set the thickness, use the setThickness() method which requires a Double value as an argument and does not return a value. For example:
pTrace->setThickness(1.5);