The parameter of a ray is the distance measured from the base point in drawing units. A positive parameter value defines the distance in the ray direction. A negative parameter value is incorrect. A zero value defines the base point. A parameter can be changed in the range from zero to positive infinity and determines the properties computed at its value (features). In examples, the pRay variable stores a pointer to the ray object.
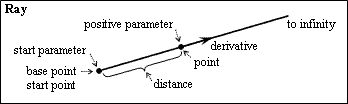
Start Parameter and Start Point
The start parameter is zero. The start point coincides with the base point. The end parameter and end point are not applicable.
To get the start parameter, use the getStartParam() method which requires a reference to a variable of the Double type in which the start parameter value must be saved as an argument and returns the start value through this argument or an error code as a result. For example:
double vStartParam;
OdResult eRes = pRay->getStartParam(vStartParam);
if(eRes == eOk)
odPrintConsoleString(L"\nStart parameter = %g", vStartParam);
To get the start point, use the getStartPoint() method which requires a reference to a variable of the OdGePoint3d type in which the start point instance must be saved as an argument and returns the computed three-dimensional point through this argument or an error code as a result. For example:
OdGePoint3d start;
OdResult eRes = pRay->getStartPoint(start);
if(eRes == eOk)
odPrintConsoleString(L"\nStart point = (%g,%g,%g)", start.x, start.y, start.z);
Note: The getEndParam(), getEndPoint(), and getArea() methods are not applicable.
Distance and Parameter
The Distance property defines the distance along the ray from the base point to the point computed at a positive parameter in drawing units. The ray object allows calculating the distance at a parameter and calculating the parameter at a distance.
To get the distance using a parameter, use the getDistAtParam() method which requires a positive parameter value specifying the point on the ray as the first argument of the Double type, requires a reference to a variable of the Double type in which the distance value must be saved as the second argument, and returns the distance through the second argument or an error code as a result. When the parameter is negative, the method returns the distance computed at a positive parameter value. For example:
double vDistance;
OdResult eRes = pRay->getDistAtParam(10.0, vDistance);
if(eRes == eOk)
odPrintConsoleString(L"\nDistance(10) = %g", vDistance);
To get the parameter using distance, use the getParamAtDist() method which requires a distance value specifying the displacement along the ray as the first argument of the Double type, requires a reference to a variable of the Double type in which the parameter value must be saved as the second argument, and returns the parameter corresponding to the distance through the second argument or an error code as a result. The distance must be a positive value, otherwise errors occur. For example:
double vParam;
OdResult eRes = pRay->getParamAtDist(30.0, vParam);
if(eRes == eOk)
odPrintConsoleString(L"\nParameter = %g", vParam);
Point and Parameter
The Point property defines the point on a ray computed at a positive parameter in three-dimensional coordinates. The ray object allows calculating the point at a parameter and calculating the parameter at a point.
To get the point using a parameter, use the getPointAtParam() method which requires a positive parameter value specifying the point on the ray as the first argument of the Double type, requires a reference to a variable of the OdGePoint3d type in which the point instance must be saved as the second argument, and returns the computed three-dimensional point through the second argument or an error code as a result. When the parameter is negative, errors occur. For example:
OdGePoint3d point;
OdResult eRes = pRay->getPointAtParam(10.0, point);
if(eRes == eOk)
odPrintConsoleString(L"\nPoint(10) = (%g,%g,%g)", point.x, point.y, point.z);
To get the parameter using a point, use the getParamAtPoint() method which requires the point instance of the OdGePoint3d type as the first argument, requires a reference to a variable of the Double type in which the parameter value must be saved as the second argument, and returns the parameter corresponding to the point through the second argument or an error code as a result. When the point is not placed on the ray, errors occur. For example:
double vParam;
OdResult eRes = pRay->getParamAtPoint(point, vParam);
if(eRes == eOk)
odPrintConsoleString(L"\nParameter = %g", vParam);
First and Second Derivatives
The First and Second Deriative properties define the first and second derivatives of a point on the ray computed at a parameter as vectors in three-dimensional coordinates. Both derivatives are constant for any point of the ray. The ray object returns the derivatives for any parameter value.
To get the first derivative, use the getFirstDeriv() method which requires a parameter value specifying the point on the ray as the first argument of the Double type, requires a reference to a variable of the OdGeVector3d type in which the first derivative vector instance must be saved as the second argument, and returns the computed three-dimensional vector through the second argument or an error code as a result. For example:
OdGeVector3d vecFirst;
OdResult eRes = pRay->getFirstDeriv(10.0, vecFirst);
if(eRes == eOk)
odPrintConsoleString(L"\nFirst derivative vector = (%g,%g,%g)", vecFirst.x, vecFirst.y, vecFirst.z);
To get the second derivative, use the getSecondDeriv() method which requires a parameter value specifying the point on the ray as the first argument of the Double type, requires a reference to a variable of the OdGeVector3d type in which the second derivative vector instance must be saved as the second argument, and returns the computed three-dimensional vector through the second argument or an error code as a result. For example:
OdGeVector3d vecSecond;
OdResult eRes = pRay->getSecondDeriv(10.0, vecSecond);
if(eRes == eOk)
odPrintConsoleString(L"\nSecond derivative vector = (%g,%g,%g)", vecSecond.x, vecSecond.y, vecSecond.z);
Note: Other methods inherited from the OdDbCurve class are not overridden in the OdDbRay class.