The lightweight polyline object uses normal, elevation, thickness, closed status, periodic status, and linetype generation status as properties to define the geometry to be drawn. In the following examples, the pLWPL variable stores a pointer to the lightweight polyline object.
Closed status
The property defines whether the lightweight polyline is closed as a Boolean value, that is, the last segment is adjacent to the first segment. If the value is True, the polyline is closed and the last vertex is connected with the first vertex. If the value is False, the polyline is open and the first vertex and last vertex are not connected. The initial value is False (open) by default.
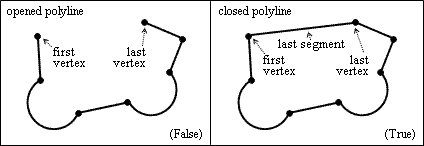
To check the closed status, use the isClosed() method which returns the status as a Boolean value. For example:
odPrintConsoleString(L"\nPolyline is %s", ((pLWPL->isClosed()) ? L"closed" : L"opened"));
To switch the closed status, use the setClosed() method which requires a Boolean value and does not return a value. For example:
// Make the closed polyline
pLWPL->setClosed(true);
// Make the opened polyline
pLWPL->setClosed(false);
Note: When the polyline is open, the last segment has type kPoint.
Periodic status
The property defines whether the lightweight polyline is a periodic curve as a Boolean value, that is, segments iterate. If the value is True, the polyline is periodic. If the value is False, the polyline is unperiodic. This property is calculated and the initial value depends on the geometry.
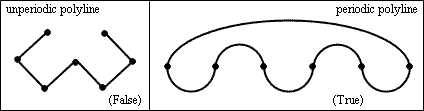
To check the periodic status, use the isPeriodic() method which returns the status as a Boolean value. For example:
odPrintConsoleString(L"\nPolyline is %s", ((pLWPL->isPeriodic()) ? L"periodic" : L"unperiodic"));
Note: The isPeriodic() method returns the close status in the default implementation, that is, the closed polyline is periodic and the opened polyline is unperiodic.
Normal
The property defines the normal to the plane in which the lightweight polyline is placed. The normal defines the orientation of the polyline in world space. The normal has the coordinates (0,0,1) by default.
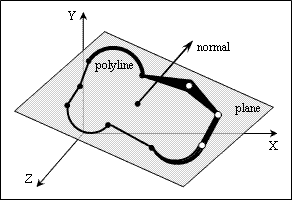
To get the normal, use the normal() method which returns the three-dimensional unit vector as an instance of the OdGeVector3d type. For example:
OdGeVector3d normal = pLWPL->normal();
odPrintConsoleString(L"\nNormal = (%g,%g,%g)", normal.x, normal.y, normal.z);
To set the normal, use the setNormal() method which requires the three-dimensional vector as an argument of the OdGeVector3d type and does not return a value. For example:
OdGeVector3d vector(0.303, 0.303, 0.707);
pLWPL->setNormal(vector);
The setNormal() method automatically converts the specified coordinates to an unit vector. For example:
pLWPL->setNormal( OdGeVector3d(2.5, 1.2, 3.4) );
OdGeVector3d result = pLWPL->normal();
odPrintConsoleString(L"\n(%g, %g, %g)", result.x, result.y, result.z);
// (0.569803, 0.273505, 0.774932)
Plane
The lightweight polyline is a planar entity. The planarity is kPlanar. The plane is oriented to (0 * X + 0 * Y + 1 * Z + 0) by default.
To get the plane, use the getPlane() method which requires a reference to a variable of the OdGePlane type in which the plane instance must be saved as the first argument, a reference to a variable of the OdDb::Planarity type in which the plane type must be saved as the second argument, and returns the plane properties through arguments and the resulting code. For example:
OdGePlane plane;
double a, b, c, d;
OdDb::Planarity planarity;
OdResult eRes = pLWPL->getPlane(plane, planarity);
if(eRes == eOk && planarity != OdDb::kNonPlanar)
{
plane.getCoefficients(a, b, c, d);
odPrintConsoleString(L"Polyline plane is (%g * X + %g * Y + %g * Z + %g)", a, b, c, d);
}
Note: The isPlanar() method returns True for the lightweight polyline entity.
Elevation
The property defines the distance from the origin of the world coordinate system to the plane of the lightweight polyline entity along the normal named as an elevation. The elevation offsets the polyline plane in world space. The initial value is zero by default.
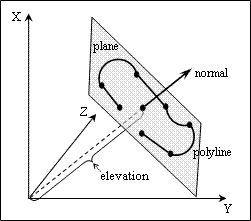
To get an elevation, use the elevation() method which returns the distance to the polyline plane as Double type. For example:
double distance = pLWPL->elevation();
OdConsoleString(L"\nElevation = %g", distance);
To set an elevation, use the setElevation() method which requires a distance to the polyline plane as an argument of Double type. For example:
pLWPL->setElevation(2.5);
Note: The ELEVATION system variable stores the default elevation value for new entities, including polylines, created in model space. The PELEVATION system variable stores the default elevation value for new entities created in paper space.
Thickness
The property defines a thickness that is the third dimension obtained by offsetting the planar polyline curve along the normal as a Double value in drawing units. A positive value defines the thickness to be drawn along the normal direction. A negative value defines the thickness to be drawn in the opposite direction from the normal. A zero value defines a polyline without thickness. The thickness is zero by default.

To get a thickness, use the thickness() method which returns the thickness as a Double value. For example:
odPrintConsoleString(L"\nPolyline thickness = %g", pLWPL->thickness());
To set a thickness, use the setThickness() method which requires a Double value as an argument. For example:
pLWPL->setThickness(1.5);
Note: The THICKNESS system variable stores the default thickness value for new entities, including polylines.
Linetype generation
The property (Boolean value) defines whether the linetype pattern of the lightweight polyline continues being drawn for each vertex or begins over again at each vertex. If the value is True, the polyline continues drawing the linetype pattern over each vertex from the first vertex to the last vertex. If the value is False, the polyline begins drawing the linetype pattern at each vertex. The initial value is True by default.

To check the linetype generation status, use the hasPlinegen() method which returns the status as a Boolean value. For example:
odPrintConsoleString(L"\nLinetype is %s each vertex", ((pLWPL->hasPlinegen()) ? L"continued for" : L"begun at"));
To switch the linetype generation status, use the setPlinegen() method which requires a Boolean value. For example:
// Make linetype generation on
pLWPL->setPlinegen(true);
// Make linetype generation off
pLWPL->setPlinegen(false);
Note: The PLINEGEN system variable stores the default linetype generation status for new polylines.
Entity coordinate system matrix
The property defines the transformation matrix that allows converting the lightweight polyline geometry between OCS and WCS. The ECS is the entity's coordinate system based on its normal and base point. A lightweight polyline takes into account only the normal. The origin is always zero in an ECS matrix. To get the matrix, use the getEcs() method that returns the transformation matrix as an instance of the OdGeMatrix3d type. For example:
OdInt16 row, col;
OdGeMatrix3d matrix;
matrix = pLWPL->getEcs();
odPrintConsoleString(L"\nMatrix:");
for(row = 0 ; row < 4 ; row++)
{
odPrintConsoleString(L"\n");
for(col = 0 ; col < 4 ; col++)
odPrintConsoleString(L"%12g ", matrix(row, col));
}
Reverse polyline
The reverseCurve() method reverses the polyline curve, so that the first vertex becomes the last vertex, and vice versa. This method does not have arguments. A first call reverses the curve, and a second call returns it to its original curve. For example:
pLWPL->reverseCurve();
Transforming to an identical 3D curve
The lightweight polyline object can be transformed into a 3D curve that is geometrically identical to the lightweight polyline. The getOdGeCurve() method requires a reference to a pointer of an instance of the OdGeCurve3d type as the first argument in which an identical 3D curve must be saved, a reference to an instance of the OdGeTol type as the second optional argument which specifies an admissible tolerance for transforming, and returns eOk if the result is successful. For example:
OdGeCurve3d* pCurve;
pLWPL->getOdGeCurve(pCurve);
Memory optimization
The lightweight polyline object can compress and decompress data allocated for vertices and segments, which optimizes memory. Compressing takes time and should not be used until all changes are complete. Decompressing expedites modification.
To compress geometry, use the minimizeMemory() method. To decompress geometry, use the maximizeMemory() method. For example:
// Compress
pLWPL->minimizeMemory();
// Decompress
pLWPL->maximizeMemory();
See Also
Working with Lightweight Polylines
Computed Lightweight Polyline Properties
Example of Working with the Lightweight Polyline Object
Copyright © 2002 – 2021. Open Design Alliance. All rights reserved.
|