Using the Ge library, you can create and modify parametric curves and surfaces. Parametric curves are defined by a function that maps an interval of the real line (possibly the entire real line) into either 2D or 3D. Surfaces are defined by a function that maps a connected subset of the UV plane (possibly the entire UV plane) into 3D space.

For every parametric entity, you can obtain a parameter value corresponding to a particular point of a curve or a surface, and conversely, you can get a point of a curve or a surface at any parameter's value. To find a parameter value by a corresponding entity's point, use the paramOf() method which is common for all curve and surface objects (as instances of the OdGeCurve3d, OdGeCurve2d or OdGeSurface classes).

For calculating a curve or surface point by a specific parameter value, the Ge library provides a mechanism that evaluates the mapping function at the parameter value. Besides the evalPoint() method, which evaluates the point on a curve or surface corresponding to the specified parameter value, there are special evaluator classes: OdGePointOnCurve2d, OdGePointOnCurve3d and OdGePointOnSurface. Usage of these classes is more efficient; they encapsulate information not only about the coordinates of the curve or surface point but also the corresponding parameter value, derivatives, normal and tangent values at the point. For curves, the parameter value is a scalar and for surfaces it's a 2D point.

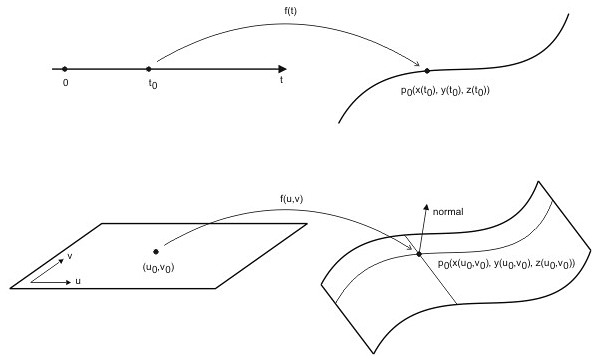
This topic demonstrates the most common usage of the evaluator classes by the example of the OdGePointOnSurface class. The functionality of OdGePointOnCurve2d and OdGePointOnCurve3d is very similar to that of OdGePointOnSurface.

To create an OdGePointOnSurface object, use the OdGePointOnSurface() constructor, which has the following four signatures:

• OdGePointOnSurface::OdGePointOnSurface() — Default constructor. Creates a point on the XY-plane with a parameter value of (0,0).
• OdGePointOnSurface::OdGePointOnSurface(const OdGePointOnSurface& source) — Creates a point on the surface cloned from a source OdGePointOnSurface object.
• OdGePointOnSurface::OdGePointOnSurface(const OdGeSurface& surface) — Creates a point on the surface for a specified surface.
• OdGePointOnSurface::OdGePointOnSurface(const OdGeSurface& surface, const OdGePoint2d& param) — Creates a point on the surface for specified surface and given parameter value.

To evaluate the surface or curve point, set a surface and parameter value for the evaluation to be done. You can pass the surface and the parameter to the constructor or use the setSurface() and setParameter() methods. For example, considering surf as a surface object and pntSurf1 as a point on the surface to be evaluated:

OdGePointOnSurface pntSurf1;
pntSurf1.setSurface(surf);
pntSurf1.setParameter(OdGePoint3d(2.0, 0, 0));

Another way to set the surface and the parameter value is to pass them to an appropriate evaluation method. Using OdGePointOnCurve2d, OdGePointOnCurve3d and OdGePointOnSurface classes, you can evaluate not only a point on a surface or curve, but also derivatives and the normal at this point. All the OdGePointOnSurface evaluation methods have the same template and three overloads:

• The point() method returns the model space point on the surface corresponding to the parameter:

   OdGePoint3d point() const — Returns the point on the surface, assuming that the surface and the parameter value have already been set.
   OdGePoint3d point(const OdGePoint2d& param) — Sets the parameter value to param (calling the setParameter() method) and then calculates the point on the surface assuming that the surface have already been set. 
   OdGePoint3d point(const OdGeSurface& surface, const OdGePoint2d& param) — Sets the surface to surface, the parameter value to param (by calling  setSurface() and setParameter()) and then calculates the point.  
   

• The normal() method calculates the normal vector at the point on the surface:

   OdGeVector3d normal() const;
   OdGeVector3d normal(const OdGePoint2d& param);
   OdGeVector3d normal(const OdGeSurface& surface, const OdGePoint2d& param);
   

• The uDeriv() method calculates the derivative (of a specified order [1-2]) of the surface in the U direction at the point corresponding to the parameter:

   OdGeVector3d uDeriv(int order) const; 
   OdGeVector3d uDeriv(int order, const OdGePoint2d& param); 
   OdGeVector3d uDeriv(int order, const OdGeSurface& surface, const OdGePoint2d& param);
   

• The vDeriv() method calculates the derivative (of a specified order [1-2]) of the surface in the V direction at the point corresponding to the parameter:

   OdGeVector3d vDeriv(int order) const; 
   OdGeVector3d vDeriv(int order, const OdGePoint2d& param); 
   OdGeVector3d vDeriv(int order, const OdGeSurface& surface, const OdGePoint2d& param);
   

• The tangentVector() method maps the specified vector to the tangent plane of the surface at the point corresponding to the parameter:

   OdGeVector3d tangentVector(const OdGeVector2d& vect) const; 
   OdGeVector3d tangentVector(const OdGeVector2d& vect, const OdGePoint2d& param);
   OdGeVector3d tangentVector(const OdGeVector2d& vect, const OdGeSurface& surface, const OdGePoint2d& param);
   

The first signature of each method takes no arguments and returns the point on the surface, assuming that the surface and the parameter value have already been set. If the surface isn't set, an exception is thrown. The second signature sets the parameter value to param by calling the setParameter(param) method and then calculates the point on the surface, assuming that the surface has already been set. The third signature sets the surface to surface, the parameter value to param (by calling setSurface(surface) and setParameter(param)), and then calculates the point.

To return the surface and parameter value, use the surface() and parameter() methods respectively. For example:

OdGePoint2d parameter = pntSurf1.parameter();
OdGeVector3d uDeriv1 = pntSurf1.uDeriv(1, surf, parameter);
OdGeVector3d vDeriv1 = pntSurf1.vDeriv(1);
OdGeVector3d normal = pntSurf1.normal();