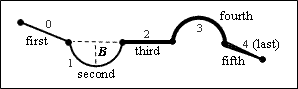
Editing Lightweight Polyline Segments

A set of lines and arcs that forms the shape of a lightweight polyline is a segment. A lightweight polyline consists of connected segments, so that the end of the current segment is the start of the next segment. The number of segments either equals the number of vertices for a closed polyline or the number of vertices minus one for an open polyline. A polyline enumerates its own segments beginning at zero (segment from first to second vertex is zero, segment from second to third vertex is one, etc.).

The lightweight polyline object provides methods for getting the type of segments, getting the parameters of linear and circular segments, getting and setting the bulge for a segment, getting and setting the start and end widths for a segment, getting a parameter for a specified point on the specified segment. In the following examples, the pLWPL variable stores a pointer to the lightweight polyline object.

Segment type

A lightweight polyline can contain both linear segments and circular segments. Additionally, a segment can be zero if the start point coincides with the end point, and a segment can be absent when it is the last segment in an open polyline or the polyline consists of one vertex.

The segment type can be determined before using it. The SegType enumeration declares the following types: kLine(=0) – linear segment, kArc(=1) – circular segment, kCoincident(=2) – zero segment (start point coincides with end point), kPoint(=3) – segment is absent (either one vertex in the polyline or a segment from the last vertex to the first vertex in an open polyline), kEmpty(=4) – empty segment.

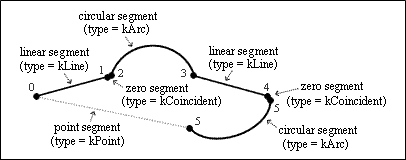
To check the segment type, use the segType() method which requires a segment index as an argument of an Integer type and returns its type as a value of the SegType enumeration. For example:


OdString about;
OdInt16 index, count = pLWPL->numVerts();

for(index = 0 ; index < count ; index++)
{
  switch( pLWPL->segType(index) )
  {
    case OdDbPolyline::kLine:	     about = L"linear";	    break;
    case OdDbPolyline::kArc:	     about = L"circular";   break;
    case OdDbPolyline::kCoincident:  about = L"zero";	    break;
    case OdDbPolyline::kPoint:	     about = L"point";      break;
    case OdDbPolyline::kEmpty:	     about = L"empty";      break;
  }
  OdConsoleString(L"\nSegment(%d) is %s", index, about.c_str());
}

To check whether a polyline contains only linear segments, use the isOnlyLines() method which returns True if all segments are linear or False if at least one segment is circular. For example:


OdConsoleString(L"\nPolyline contains %s", ((pLWPL->isOnlyLines()) ? L"only lines" : L"lines&arcs"));

Getting parameters of a linear segment

A lightweight polyline allows getting the line parameters for linear segments in OCS and WCS. The OdGeLineSeg2d class defines the parameters for two-dimensional linear segment. The OdGeLineSeg3d class defines the parameters for three-dimensional linear segments.

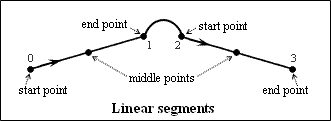
To get a linear segment, use the getLineSegAt() method which requires the segment index as the first argument of the Integer type, and a reference either to an instance of the OdGeLineSeg2d type to get two-dimensional linear segment parameters in OCS or an instance of the OdGeLineSeg3d type to get three-dimensional linear segment parameters in WCS as the second argument in which parameters must be saved, and returns them through the second argument. For example:


OdGePoint2d start2d, end2d, mid2d;
OdGePoint3d start3d, end3d, mid3d;

OdGeLineSeg2d line2d;
OdGeLineSeg3d line3d;

OdInt16 index, count = pLWPL->numVerts();

if(!pLWPL->isClosed()) count--;

for(index = 0 ; index < count ; index++)
{
  pLWPL->getLineSegAt(index, line2d);

  start2d = line2d.startPoint();
  end2d = line2d.endPoint();
  mid2d = line2d.midPoint();
  
  OdConsoleString(L"\n2D Line Segment (%d) passes in OCS from (%g,%g) to (%g,%g) via (%g,%g)", 
                  index, start2d.x, start2d.y, end2d.x, end2d.y, mid2d.x, mid2d.y);

  pLWPL->getLineSegAt(index, line3d);
  
  start3d = line3d.startPoint();
  end3d = line3d.endPoint();
  mid3d = line3d.midPoint();
  
  OdConsoleString(L"\n3D Line Segment (%d) passes in WCS from (%g,%g,%g) to (%g,%g,%g) via (%g,%g,%g)", 
                  index, start3d.x, start3d.y, start3d.z, end3d.x, end3d.y, end3d.z, mid3d.x, mid3d.y, mid3d.z);
}

Note: The getLineSegAt() method throws an exception when the specified segment does not have type kLine.

Getting parameters of a circular segment

A lightweight polyline allows getting the arc parameters for circular segments in OCS and WCS. The OdGeArcSeg2d class defines the parameters for two-dimensional circular segments. The OdGeArcSeg3d class defines the parameters for three-dimensional circular segments.

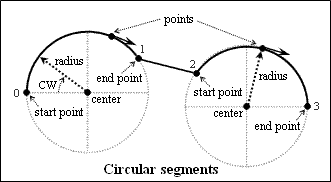
To get a circular segment, use the getArcSegAt() method which requires the segment index as the first argument of an Integer type, and a reference either to an instance of the OdGeArcSeg2d type to get two-dimensional circular segment parameters in OCS or an instance of the OdGeArcSeg3d type to get three-dimensional circular segment parameters in WCS as the second argument in which parameters must be saved, and returns them through the second argument. For example:


OdGePoint2d start2d, end2d, center2d, radius2d;
OdGePoint3d start3d, end3d, center3d, radius3d;
OdGeVector3d normal;

OdGeArcSeg2d arc2d;
OdGeArcSeg3d arc3d;

OdInt16 index, count = pLWPL->numVerts();

if(!pLWPL->isClosed()) count--;

for(index = 0 ; index < count ; index++)
{
  pLWPL->getArcSegAt(index, arc2d);

  end2d    = arc2d.endPoint();
  start2d  = arc2d.startPoint();
  center2d = arc2d.center();
  radius2d = arc2d.radius();
  
  OdConsoleString(L"\n2D Arc Segment (%d) R=%g passes in OCS from (%g,%g) to (%g,%g) center (%g,%g)", 
                  index, radius2d, start2d.x, start2d.y, end2d.x, end2d.y, center2d.x, center2d.y);

  pLWPL->getArcSegAt(index, arc3d);
  
  end3d    = arc3d.endPoint();
  start3d  = arc3d.startPoint();
  normal   = arc3d.normal();
  center3d = arc3d.center();
  radius3d = arc3d.radius();
  
  OdConsoleString(L"\n3D Arc Segment (%d) R=%g passes in WCS from (%g,%g,%g) to (%g,%g,%g) center (%g,%g,%g) normal (%g,%g,%g)", 
                  index, radius3d, start3d.x, start3d.y, start3d.z, end3d.x, end3d.y, end3d.z, 
                  center3d.x, center3d.y, center3d.z, normal.x, normal.y, normal.z);
}

Note: The getArcSegAt() method throws an exception when the specified segment does not have type kArc.

Segment bulge

A bulge is the parameter that specifies the curvature of circular arcs as the ratio between the length (D) of the linear segment from the start point to the end point and two times the length (H) of the perpendicular segment from the middle point of the linear segment to the middle point on the circular segment (B = 2H/D). A positive bulge rotates the arc from the start point to the end point counterclockwise. A negative bulge rotates the arc from the start point to the end point clockwise.

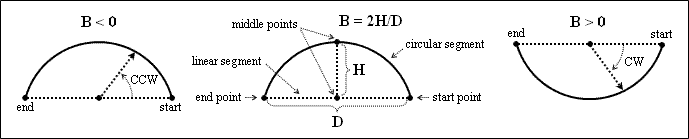
When a bulge is a zero (0.0), the segment is a straight line. When a bulge is one (1.0), the segment is a half-circle. When a bulge is from 0.0 to 1.0, the segment is a circular arc.

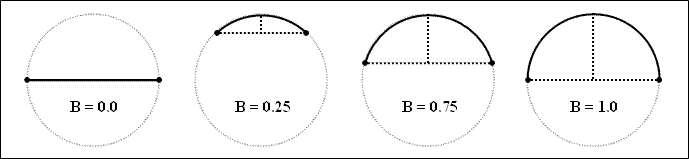
The property defines the bulges for an each segment of a polyline. The initial values are zero by default.

To get a bulge of a segment, use the getBulgeAt() method which requires an index of a segment as an argument of Integer type and returns its bulge as a Double type. For example:


double  bulge;
OdInt16 index, count = pLWPL->numVerts();

if(!pLWPL->isClosed()) count--;

for(index = 0 ; index < count ; index++)
{
  bulge = pLWPL->getBulgeAt( index );
  OdConsoleString(L"\nBulge(%d) = %g", index, bulge);
}

To set a bulge for a segment, use the setBulgeAt() method which requires an index of a segment as the first argument (Integer type) and the bulge value as the second argument (Double type). For example:


pLWPL->setBulgeAt(0, 0.25);
pLWPL->setBulgeAt(1, -0.5);

To check whether a polyline has bulges, use the hasBulges() method which returns True if at least one segment has a non-zero bulge or False if all segments have a zero bulge. For example:


OdConsoleString(L"\nPolyline has %s bulges", ((pLWPL->hasBulges()) ? L"non-zero" : L"only zero"));

Segment width

A lightweight polyline can have constant or variable width both for linear and circular segments. A lightweight polyline fills inside segments using entity color. The segment shape is defined by the start width and end width. When start and end widths are equal, the segment has a consistent shape. When start and end widths are different, the segment has a taper shape. When start and end widths are zero, the segment is a thin line.

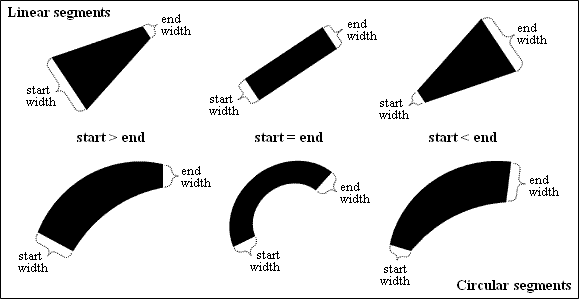
The property defines the widths for each segment of a polyline. The initial values are zero by default.

To get widths of a segment, use the getWidthsAt() method which requires an index of a segment as the first argument (Integer type), a reference to the variable (Double type) in which the start width must be saved as the second argument, a reference to the variable (Double type) in which the end width must be saved as the third argument, and returns widths through the second and third arguments. For example:


double  width_start, width_end;
OdInt16 index, count = pLWPL->numVerts();

if(!pLWPL->isClosed()) count--;

for(index = 0 ; index < count ; index++)
{
  pLWPL->getWidthsAt( index, width_start, width_end );
  OdConsoleString(L"\nWidth (%d) from (%g) to (%g)", index, width_start, width_end);
}

To set widths for a segment, use the setWidthsAt() method which requires an index of a segment as the first argument (Integer type), start width as the second argument (Double type), and end width as the third argument (Double type). For example:


pLWPL->setWidthsAt(0, 0.1, 1.0);
pLWPL->setWidthsAt(1, 1.0, 0.5);
pLWPL->setWidthsAt(2, 0.5, 0.9);
pLWPL->setWidthsAt(3, 0.9, 0.1);

To check whether a polyline has widths, use the hasWidth() method which returns True if at least one segment has a non-zero start width or non-zero end width, or False if all segments have zero widths. For example:


OdConsoleString(L"\nPolyline has %s widths", ((pLWPL->hasWidth()) ? L"non-zero" : L"only zero"));

Constant width

The property defines the constant width which defines the same start and end widths for all segments. The initial value is zero by default.

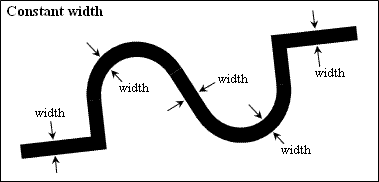
To get a constant width, use the getConstantWidth() method which returns the width which is common for all segments as a Double type. For example:


double width = pLWPL->getConstantWidth();

OdConsoleString(L"\nConstant width = %g", width);

To set a constant width, use the setConstantWidth() method which requires a width value as an argument of Double type. For example:


pLWPL->setConstantWidth(0.25);

Note: The PLINEWID system variable stores the default width value for new polylines.

Getting a parameter at a point

A lightweight polyline provides the ability to determine whether a linear or circular segment lies on a point and to get the curve parameter if the specified point lies on the specified segment. The parameter is changed from 0.0 to 1.0 for each segment. If a point lies on the segment, the parameter value moves from the previous index to the next index value.

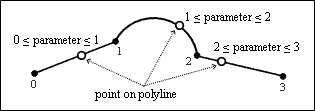
To catch a point of a lightweight polyline, use the onSegAt() method which requires an index of a segment as the first argument (Integer type), a two-dimensional point as the second argument (OdGePoint2d type), a reference to the variable (Double type) as the third argument in which the polyline parameter must be saved if the specified point lies on the specified segment. This method passes the parameter through the third argument and returns True if the specified point lies on the specified segment or False if the specified point lies outside the specified segment. For example:


double param;
OdInt16 index = 0;
OdGePoint2d point2d(2.4, 1.2);

if(pLWPL->onSegAt( index, point2d, param ))
  OdConsoleString(L"\nPoint lies on the segment(%d) with parameter = %g", index, param);
else
  OdConsoleString(L"\nPoint outs the segment");

Adding a segment

The addVertexAt() method adds a new segment together with a new vertex using default parameters: bulge is zero, and start and end widths are absent. To specify the segment properties, pass the bulge value as the third argument, start width value as the forth argument, and end width value as fifth argument. For example:


pLWPL->addVertexAt( 0, OdGePoint2d(1.4, 1.5),   0.5, 0.3, 0.8 );
pLWPL->addVertexAt( 1, OdGePoint2d(6.4, 2.1),  -0.5, 0.8, 0.4 );
pLWPL->addVertexAt( 2, OdGePoint2d(4.6, 5.2),  0.25, 0.4, 0.2 );
pLWPL->addVertexAt( 3, OdGePoint2d(2.5, 3.5), -0.25, 0.2, 0.2 );