A NURBS surface consists of connected quadrangular fragments (spans). Each fragment is defined by four control points, which are used to define the track along which the B-splines are drawn.
NURBS surface objects provide methods for getting the number of control vertices,
getting and changing the coordinates of control points, inserting and deleting
control points, getting and setting weights, and can be open or closed, periodic,
planar, etc. To see how to work with control points, see Working
with Control Points of NURBS Surfaces. In the following examples, the pNurbSurf
variable stores a pointer to the NURBS surface object.
Planar Status
A NURBS surface is called planar if all of its points lie in the same plane.
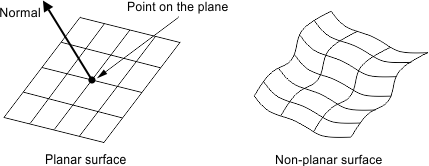
To find out whether a NURBS surface is planar, use the isPlanar() method, which
requires three parameters: a bool value through which the isPlanar flag is returned, an OdGePoint3d object through which the point on the surface is returned (if the surface is planar), and an OdGeVector3d object through which
the surface normal is returned (if the surface is planar).
For example:
bool bIsPlanar;
OdGePoint3d pntSurf;
OdGeVector3d normal;
pNurbSurf->isPlanar(bIsPlanar, pntSurf, normal);
odPrintConsoleString(L"\nSurface is %s", ((bIsPlanar) ? L"planar" : L"non-planar"));
if (bIsPlanar)
{
odPrintConsoleString(L"\nPoint on surface: (%f; %f; %f)", pntSurf.x, pntSurf.y, pntSurf.z);
odPrintConsoleString(L"\nNormal: (%f; %f; %f)", normal.x, normal.y, normal.z);
}
Closed Status
A NURBS surface can be closed in the u- or v-direction:
- Closed in the u-direction — Surface is closed by drawing quadrangular figures in a row between the last and first rows.
- Closed in the v-direction — Surface is closed by drawing quadrangular figures in a column between the last and first columns.
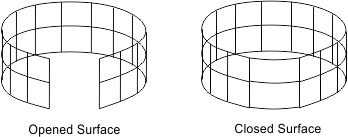
To check the closed status in the u- and v-directions, use the isClosedInU()
and isClosedInV() methods respectively, which require one bool value through
which the isClosed flag is returned.
For example:
bool bIsClosedU, bIsClosedV;
pNurbSurf->isClosedInU(bIsClosedU);
pNurbSurf->isClosedInV(bIsClosedV);
odPrintConsoleString(L"\nSurface is %s on u-direction", ((bIsClosedU) ? L"closed" : L"opened"));
odPrintConsoleString(L"\nSurface is %s on v-direction", ((bIsClosedV) ? L"closed" : L"opened"));
Degree of a NURBS Surface
The degree is a positive integer value that controls the number of points per interval that are available for modeling. For example, a degree-1 curve means that two control points are connected by a straight line. A degree-2 curve means that there is one bend between the control points, and so on. The degree in the u- and v- directions can be different.
To get the NURBS surface degree in the u- and v-direction, use the getDegreeInU()
and getDegreeInV() methods respectively, which require one integer parameter
through which the degree is returned.
For example:
int iDegreeU, iDegreeV;
pNurbSurf->getDegreeInU(iDegreeU);
pNurbSurf->getDegreeInV(iDegreeV);
odPrintConsoleString(L"\nDegree on u-direction is %i",iDegreeU);
odPrintConsoleString(L"\nDegree on v-direction is %i",iDegreeV);
Rational Status
A NURBS surface is called rational when it has weighted control points.
To find out whether a NURBS surface is rational, use the isRational() method,
which requires one bool value through which the isRational flag is returned.
For example:
bool bIsRational;
pNurbSurf->isRational(bIsRational);
odPrintConsoleString(L"\nSurface is %s", ((bIsRational) ? L"rational" : L"non-rational"));
Periodic Status
A NURBS surface can be periodic in the u- and v-direction. If a surface is closed in one direction (opposite sides are the same line in object space) and the parameterization and derivatives also match at these boundaries, the surface is periodic in the parameter direction.
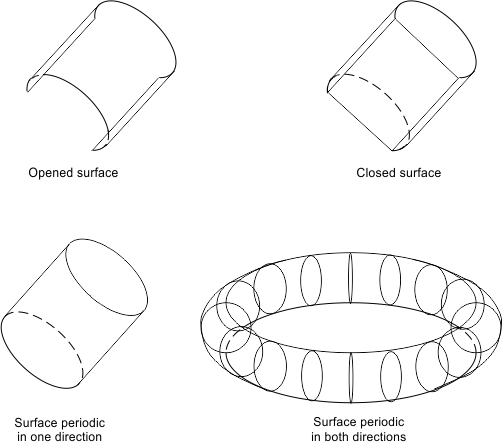
To find out whether a NURBS surface is periodic in the u- or v-direction, use
the isPeriodicInU() and isPeriodicInV() methods respectively, which require
one bool value through which the isPeriodic flag is returned.
For example:
bool bIsPeriodicU, bIsPeriodicV;
pNurbSurf->isPeriodicInU(bIsPeriodicU);
pNurbSurf->isPeriodicInV(bIsPeriodicV);
odPrintConsoleString(L"\nSurface is %s on u-direction", ((bIsPeriodicU) ? L"periodic" : L"aperiodic"));
odPrintConsoleString(L"\nSurface is %s on v-direction", ((bIsPeriodicV) ? L"periodic" : L"aperiodic"));
Get the Period
To get the period of a surface in the u- or v-direction, use the getPeriodInU()
and getPeriodInV() methods respectively, which require one double parameter
through which the period is returned.
For example:
double dPeriodU, dPeriodV;
pNurbSurf->getPeriodInU(dPeriodU);
pNurbSurf->getPeriodInV(dPeriodV);
odPrintConsoleString(L"\nPeriod on u-direction is %f",dPeriodU);
odPrintConsoleString(L"\nPeriod on v-direction is %f",dPeriodV);
Normal
A NURBS surface can have many normals if it is non-planar. To get the normal
for a specified point on a surface, use the getNormal() method, which requires
three parameters: two double values to specify the u and v parameters of the
point and an OdGeVector3d object through which the normal is returned.
For example:
double dU = 1.3;
double dV = 0.7;
OdGeVector3d normal;
pNurbSurf->getNormal(dU, dV, normal);
odPrintConsoleString(L"\nNormal on parameters [%f; %f]: (%f; %f; %f)", dU, dV, normal.x, normal.y, normal.z);
Get Isolines
You can get the isolines that form a surface in the u- and v-directions. To
do so, use the getIsolineAtU() and getIsolineAtV() methods respectively, which
require two parameters: one double value to specify the u or v parameter and
an OdDbCurvePtrArray object through which the isoline segments are returned.
For example:
double dU = 2.1;
double dV = 1.8;
OdDbCurvePtrArray lineSegmentsU, lineSegmentsV;
pNurbSurf->getIsolineAtU(dU, lineSegmentsU);
pNurbSurf->getIsolineAtV(dV, lineSegmentsV);
Work with Knots
NURBS are parametric curves, which means that for a curve defined by function
P(u) there is always some point P on the curve for a particular parameter u.
The curve is drawn while u changes its value from the initial value umin
to umax. Knots are defined in the parameter space of such a curve.
A knot vector is an array of knots of a curve. A curve is defined by a set of
polynomials. The knot vector determines the borders of the polynomials in the
parameter range.
For more details about the knot vector, see Working with NURBS Data.
To get the number of knots in the u- or v-direction, use the getNumberOfKnotsInU()
and getNumberOfKnotsInV() methods respectively, which require one integer parameter
through which the number of knots is returned.
For example:
int iKnotU;
int iKnotV;
pNurbSurf->getNumberOfKnotsInU(iKnotU);
pNurbSurf->getNumberOfKnotsInV(iKnotV);
odPrintConsoleString(L"\nNumber of knots on u-direction is %i",iKnotU);
odPrintConsoleString(L"\nNumber of knots on v-direction is %i",iKnotV);
To get the array of knots in the u- or v-direction, use the getUKnots() and
getVKnots() methods respectively, which require one OdGeKnotVector object through
which the knot vector is returned.
For example:
OdGeKnotVector knotsU, knotsV;
pNurbSurf->getUKnots(knotsU);
pNurbSurf->getVKnots(knotsV);
for (int i = 0; i < knotsU.logicalLength(); i++)
{
odPrintConsoleString(L"\nUKnot %d is %f", i, knotsU[i]);
}
for (int i = 0; i < knotsV.logicalLength(); i++)
{
odPrintConsoleString(L"\nVKnot %d is %f", i, knotsV[i]);
}
To insert a new knot to a specified location in the u- or v-direction, use
the InsertKnotAtU() or InsertKnotAtV() methods respectively, which require one
double parameter to specify the place of the new knot. The knot insertion doesn't
modify the shape of the surface. It adds a new row or column of control
points in the v- or u-direction and adjusts the local control point's location.
For example:
pNurbSurf->InsertKnotAtU(2.1);
pNurbSurf->InsertKnotAtV(1.5);
Number of Spans
To get the number of spans (simple patches that form the shape of a NURBS surface)
in the u- or v-direction, use the getNumberOfSpansInU() and getNumberOfSpansInV()
methods respectively, which require one integer value through which the number
of spans is returned.
For example:
int numSpanU, numSpanV;
pNurbSurf->getNumberOfSpansInU(numSpanU);
pNurbSurf->getNumberOfSpansInV(numSpanV);
odPrintConsoleString(L"\nSpans number on u-direction is %f",numSpanU);
odPrintConsoleString(L"\nSpans number on v-direction is %f",numSpanV);
Get and Set Common Data
To get common NURBS data such as the array of control points, the number of
control points in the u- and v-directions, degree, weights, and so on, use the
get() method, which requires nine parameters through which this data is
returned: two integer values to return the degree in the u- and v-directions,
a bool value to return the is rational flag, two integer values to return
the number of points in the u- and v-directions, an OdGePoint3dArray object
to return the array of control points, an OdGeDoubleArray object to return the
array of weights, and two OdGeKnotVector objects to return the knots in the
u- and v-directions.
For example:
int uDegree, vDegree, numCntrlU, numCntrlV;
bool bRational;
OdGePoint3dArray cntrlPtsArr;
OdGeDoubleArray weights;
OdGeKnotVector uKnots, vKnots;
// Get common data
pNurbSurf->get(uDegree, vDegree, bRational, numCntrlU, numCntrlV, cntrlPtsArr, weights, uKnots, vKnots);
// Display some properties
odPrintConsoleString(L"\nNumber of control points on u-direction is %f",numCntrlU);
odPrintConsoleString(L"\nNumber of control points on v-direction is %f",numCntrlV);
To set common NURBS data such as an array of control points, the number of
control points in the u- and v-directions, degree, weights, and so on, use the
set() method, which requires nine parameters: two integer values to set the
degree in the u- and v-directions, a bool value to set the is rational flag,
two integer values to set the number of points in the u- and v-directions, an
OdGePoint3dArray object to set the array of control points, an OdGeDoubleArray
object to set the array of weights, and two OdGeKnotVector objects to set the
knots in the u- and v-directions. For knots, use these rules:
- Number of knots must be: nCP + degree + 1.
- The first and last (degree + 1) knots must be equal.
For example:
int uDegree = 2;
int vDegree = 3;
int numCntrlU = 4;
int numCntrlV = 5;
bool bRational = true;
int numCntrl = numCntrlU * numCntrlV;
OdGePoint3d arrCP[] = {OdGePoint3d(4, 0, 2), OdGePoint3d(7, 0, 1), OdGePoint3d(9, 0, 3), OdGePoint3d(10, 0, 2), OdGePoint3d(12, 0, 1),
OdGePoint3d(4, 3, -1), OdGePoint3d(7, 3, -1), OdGePoint3d(9, 2, 0), OdGePoint3d(10, 1, -1), OdGePoint3d(12, 2, -3),
OdGePoint3d(4, 5, 0), OdGePoint3d(7, 5, 2), OdGePoint3d(9, 4, 2), OdGePoint3d(10, 5, 2), OdGePoint3d(12, 4, -1),
OdGePoint3d(4, 7, 3), OdGePoint3d(7, 7, 4), OdGePoint3d(9, 6, 3), OdGePoint3d(10, 7, 4), OdGePoint3d(12, 5, 1)};
OdGePoint3dArray cntrlPtsArr;
cntrlPtsArr.resize(numCntrl);
for (int i = 0; i < numCntrl; i++)
{
cntrlPtsArr.push_back(arrCP[i]);
}
double arrWeights[] = {2, 3, 3, 4, 2, 3, 2, 3, 3, 4, 2, 3, 2, 3, 3, 4, 2, 3, 1, 2};
OdGeDoubleArray weights;
weights.resize(numCntrl);
for (int i = 0; i < numCntrl; i++)
{
weights.push_back(arrWeights[i]);
}
double arrUKnots[] = {0, 0, 0, 3, 5, 5, 5};
double arrVKnots[] = {0, 0, 0, 0, 2, 4, 4, 4, 4};
OdGeKnotVector uKnots(sizeof(arrUKnots) / sizeof(double), arrUKnots);
OdGeKnotVector vKnots(sizeof(arrVKnots) / sizeof(double), arrVKnots);
// Set common data
pNurbSurf->set(uDegree, vDegree, bRational, numCntrlU, numCntrlV, cntrlPtsArr, weights, uKnots, vKnots);
Note: Setting the data can be done only via the SpaModeler.
See Also
Copyright © 2002 – 2020. Open Design Alliance. All rights reserved.
|