Specific Helix Properties

The helix object uses a start point, axis point, axis vector, base radius, top radius, total height, turn height, number of turns, and twist direction properties to define the geometry to be drawn. In the following examples, the pHelix variable stores a pointer to the helix object.

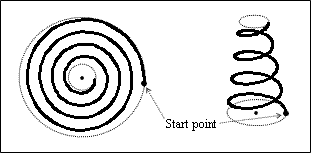
Start Point

The Start Point property defines the point from which the spiral curve starts using three-dimensional world coordinates. The start point and axis point are placed in the same plane. The start point influences the base radius and recalculates it relative to the axis point. If the start point coincides with the axis point, the base radius is zero. The start point has the coordinates (0,0,0) by default.

To get the start point, use the startPoint() method which does not have arguments and returns the three-dimensional point as an instance of the OdGePoint3d type. For example:


OdGePoint3d start = pHelix->startPoint();
odPrintConsoleString(L"\nPosition = (%g,%g,%g)", start.x, start.y, start.z);

To set the start point, use the setStartPoint() method which requires the three-dimensional point as an argument of the OdGePoint3d type and does not return a value. For example:


OdGePoint3d point(4.8, 6.2, 1.8);
pHelix->setStartPoint(point);

Note: The setStartPoint() method rotates the spiral curve around the axis when the start point moves in the base plane.

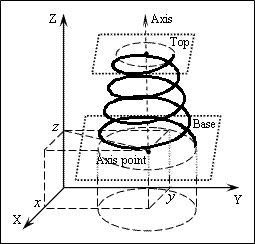
Axis Point

The Axis Point property defines the start position of the axis along which the spiral curve is drawn using three-dimensional world coordinates. The axis point coincides with the center of the circle that defines the base radius of the spiral curve. The axis point influences the helix position. If the axis point coincides with the start point, the base radius is zero. The axis point has the coordinates (0,0,0) by default.

To get the axis point, use the axisPoint() method which does not have arguments and returns the three-dimensional point as an instance of the OdGePoint3d type. For example:


OdGePoint3d position = pHelix->axisPoint();
odPrintConsoleString(L"\nPosition = (%g,%g,%g)", position.x, position.y, position.z);

To set the axis point, use the setAxisPoint() method which requires a three-dimensional point as the first mandatory argument of the OdGePoint3d type and a moveable sign as a second optional argument of Boolean type; it does not return a value. If the moveable sign is True, the method moves the axis point together with start point to a new position, storing the base radius as a constant, that is, it relocates both points with the same offset. If the moveable sign is False, the method moves the axis point, storing the location of the start point, and recalculates the base radius. The moveable sign is True by default. For example:


// Relocate the axis point storing the base radius (move start point)
OdGePoint3d point(2.6, 3.4, 1.8);
pHelix->setAxisPoint(point, true);

// Relocate the axis point storing the start point (modify the base radius)
OdGePoint3d point(2.6, 3.4, 1.8);
pHelix->setAxisPoint(point, false);

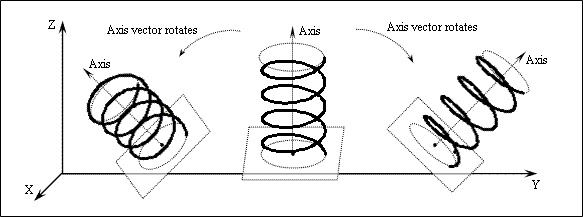
Axis Vector

The Axis Vector property defines the vector of the axis along which the spiral curve is drawn. The axis vector defines the orientation of the spiral curve in world space. The axis vector has the coordinates (0,0,1) by default.

To get the axis vector, use the axisVector() method which does not have arguments and returns the three-dimensional vector as an instance of the OdGeVector3d type. For example:


OdGeVector3d axis = pHelix->axisVector();
odPrintConsoleString(L"\nAxis vector = (%g,%g,%g)", axis.x, axis.y, axis.z);

To set the axis vector, use the setAxisVector() method which requires a three-dimensional vector as an argument of the OdGeVector3d type and does not return a value. For example:


OdGeVector3d vector(0.505, 0.303, 0.707);
pHelix->setAxisVector(vector);

Note: The setAxisVector() method automatically converts the specified coordinates to a unit vector. For example:


pHelix->setAxisVector( OdGeVector3d(2.5, 1.2, 3.4) );
OdGeVector3d result = pHelix->axisVector();
odPrintConsoleString(L"\n(%g, %g, %g)", result.x, result.y, result.z);    // (0.569803, 0.273505, 0.774932)

Plane

When the total height is zero, the helix is a planar entity. The plane is oriented to (0·X + 0·Y + 1·Z + 0) by default.

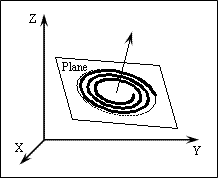
To check whether the helix is planar, use the isPlanar() method that returns True when the helix is planar or False when the helix is non-planar.


odPrintConsoleString(L"\nHelix is %s", ((pHelix->isPlanar()) ? L"planar" : L"non-planar"));

To get the helix plane, use the getPlane() method which requires a reference to a variable of the OdGePlane type in which the plane instance must be saved as the first argument, a reference to a variable of the OdDb::Planarity type in which the plane type must be saved as the second argument, and returns the plane properties through arguments and the resulting code. For example:


OdGePlane plane;
double a, b, c, d;
OdDb::Planarity planarity;

OdResult eRes = pHelix->getPlane(plane, planarity);

if(eRes == eOk && planarity != OdDb::kNonPlanar)
{
  plane.getCoefficients(a, b, c, d);
  odPrintConsoleString(L"Helix plane is (%g * X + %g * Y + %g * Z + %g)", a, b, c, d);
}

Base Radius

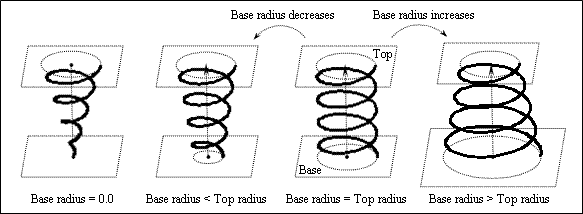
The Base Radius property defines the base radius from which the spiral curve begins as a positive double value in drawing units. The base radius influences the turn slope. If the base radius equals the top radius, the turn slope is zero and the spiral curve has a cylindrical shape. If the base radius is more than the top radius, the turn slope is negative and the spiral curve has a convergent, cone shape. If the base radius is less than the top radius, the turn slope is positive and the spiral curve has a divergent, cone shape. If the base radius is zero, the spiral curve starts from the axis point. The base radius is 0.0 by default.

To get the base radius, use the baseRadius() method which does not have arguments and returns the base radius as a positive double value. For example:


odPrintConsoleString(L"\nBase radius = %g", pHelix->baseRadius());

To set the base radius, use the setBaseRadius() method which requires a double value as an argument and does not return a value. For example:


pHelix->setBaseRadius(1.5);

Note: If the specified value is negative, the setBaseRadius() method changes the X-coordinate of the start point to the opposite value and sets the base radius to the positive value.

Top Radius

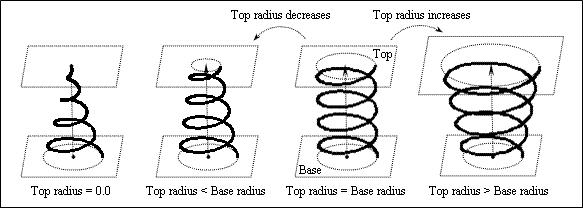
The Top Radius property defines the top radius to which the spiral curve ends as a positive double value in drawing units. The top radius influences the turn slope. If the top radius equals the base radius, the turn slope is zero and the spiral curve has a cylindrical shape. If the top radius is more than the base radius, the turn slope is positive and the spiral curve has a divergent, cone shape. If the top radius is less than the base radius, the turn slope is negative and the spiral curve has a convergent, cone shape. If the top radius is zero, the spiral curve ends in the end of the axis. The top radius is 1.0 by default.

To get the top radius, use the topRadius() method which does not have arguments and returns the top radius as a positive double value. For example:


odPrintConsoleString(L"\nTop radius = %g", pHelix->topRadius());

To set the top radius, use the setTopRadius() method which requires a double value as an argument and does not return a value. For example:


pHelix->setTopRadius(1.5);

Note: If the specified value is negative, the setTopRadius() method sets the top radius to a positive value.

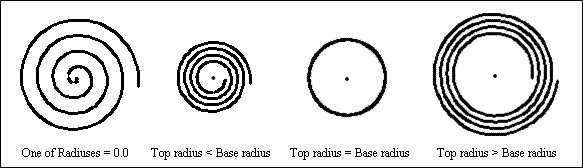
When the height is zero, the helix entity is planar and the base radius and top radius define either the divergent or convergent circular shape for the spiral curve. When the base radius equals the top radius, the planar helix transforms into a circle or arc.

Turn Slope

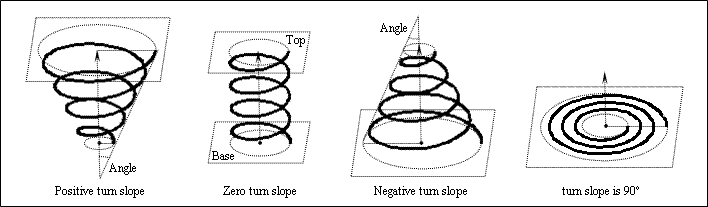
The Turn Slope property defines the angle in radians as a double value in the range –PI/2 to +PI/2 on which the helix expands or narrows along the axis from the base to the top. If the turn slope is positive, the spiral curve has a divergent, cone shape along the axis and the top radius is more than base radius. If the turn slope is negative, the spiral curve has a convergent, cone shape along the axis and the base radius is more than the top radius. If the turn slope is zero, the spiral curve has the cylindrical shape along the axis and its radiuses are equal. If the turn slope is a right angle, that is PI/2, the helix is planar. The turn slope is 0.785398 (45º) by default.

To get the turn slope, use the turnSlope() method which does not have arguments and returns the angle as a double value. For example:


odPrintConsoleString(L"\nTurn slope = %g", pHelix->turnSlope());

Note: The helix object does not have a method to set the turn slope; this property is read-only.

Constrain

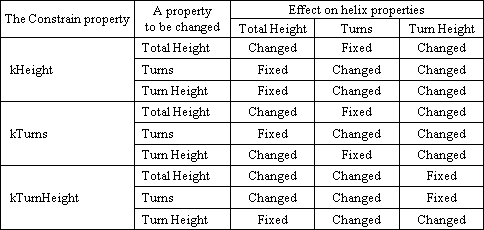
The Constrain property defines the behavior of the spiral curve when its properties are changed. This property specifies whether Total Height, Turn Height, and Turns are constant when other properties change. The constrain property is an integer value defined by the OdDbHelix::ConstrainType enumerator which defines three values: kTurnHeight (=0), kTurns (=1), and kHeight (=2) to provide the following behavior:

To get the constrain property, use the constrain() method which does not have arguments and returns the ConstrainType value. For example:


switch( pHelix->constrain() )
{
  case OdDbHelix::kTurnHeight:
       odPrintConsoleString(L"\nConstrain = kTurnHeight");
       break;
  case OdDbHelix::kTurns:
       odPrintConsoleString(L"\nConstrain = kTurns");
       break;
  case OdDbHelix::kHeight:
       odPrintConsoleString(L"\nConstrain = kHeight");
       break;
}

To set the constrain property, use the setConstrain() method which requires an integer value as an argument and does not return a value. For example:


// Set to kTurns
pHelix->setConstrain( OdDbHelix::kTurns );

// Set to kHeight
pHelix->setConstrain( OdDbHelix::kHeight );

// Set to kTurnHeight
pHelix->setConstrain( OdDbHelix::kTurnHeight );

Note: The constrain type is kTurnHeight by default.

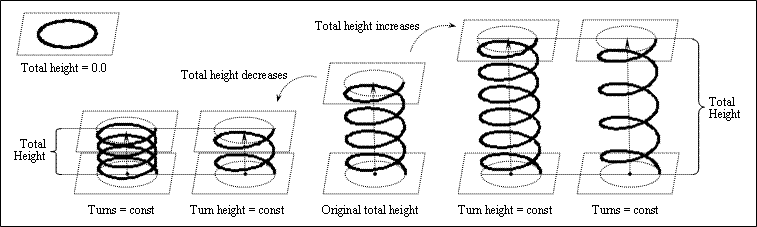
Total Height

The Total Height property defines the total height of the spiral curve in drawing units from the base plane to the top plane along the axis vector. This property influences either the number of turns or the turn height, depending on the constrain property:

If the constrain property is set to kTurnHeight, the helix object fixes the turn height as a constant and amplifies the number of turns when the total height increases or reduces the number of turns when the total height decreases.
If the constrain property is set to kTurns or kHeight, the helix object fixes the number of turns as a constant and raises the turn height when the total height increases or descends the turn height when the total height decreases.

If the total height is zero, the spiral curve is planar (a circle or arc). The total height is 1.0 by default.

To get the total height, use the height() method which does not have arguments and returns the height as a positive double value. For example:


odPrintConsoleString(L"\nTotal height = %g", pHelix->height());

To set the total height, use the setHeight() method which requires a double value as an argument and does not return a value. For example:


pHelix->setHeight(4.8);

Note: If the specified value is negative, the setHeight() method changes the axis vector to the opposite direction and sets the height to a positive value. For example:


OdGeVector3d direct1 = pHelix->axisVector();
double value1 = pHelix->height();

// Before: H = 4.8, Axis to (0,0,1)
odPrintConsoleString(L"\nBefore: H = %g, Axis to (%g,%g,%g)", value1, direct1.x, direct1.y, direct1.z);

pHelix->setHeight(-4.8);

OdGeVector3d direct2 = pHelix->axisVector();
double value2 = pHelix->height();

// After: H = 4.8, Axis to (0,0,-1)
odPrintConsoleString(L"\nAfter: H = %g, Axis to (%g,%g,%g)", value2, direct2.x, direct2.y, direct2.z);

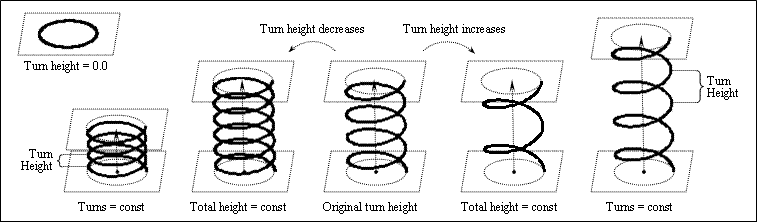
Turn Height

The Turn Height property defines the height of one full turn or distance between turns for the spiral curve in drawing units. This property influences either the number of turns or the total height, depending on the constrain property:

If the constrain property is set to kTurns, the helix object fixes the number of turns as a constant and raises the total height when the turn height increases or descends the total height when the turn height decreases.
If the constrain property is set to kHeight or kTurnHeight, the helix object fixes the total height as a constant and reduces the number of turns when the turn height increases or amplifies the number of turns when the turn height decreases.

If the turn height is zero, the spiral curve is planar. The turn height is 1.0 by default.

To get the turn height, use the turnHeight() method which does not have arguments and returns the height as a double value. For example:


odPrintConsoleString(L"\nTurn height = %g", pHelix->turnHeight());

To set the turn height, use the setTurnHeight() method which requires a positive double value as an argument and does not return a value. For example:


pHelix->setTurnHeight(1.2);

Note: The specified value must be positive.

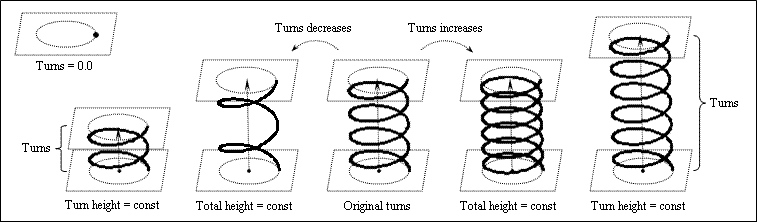
Turns

The Turns property defines the number of turns (revolutions) for the spiral curve, and the value can be a fraction. This property influences either the total height or the turn height, depending on the constrain property:

If the constrain property is set to kTurnHeight, the helix object fixes the turn height as a constant and raises the total height when the number of turns increases or descends the total height when the number of turns decreases.
If the constrain property is set to kHeight or kTurns, the helix object fixes the total height as a constant and descends the turn height when the number of turns increases or raises the turn height when the number of turns decreases.

If the turns property is zero, the total height equals zero, and the spiral curve transforms into a point. The number of turns is 1.0 by default.

To get the turns property, use the turn() method which does not have arguments and returns the number of turns (revolutions) as a double value. For example:


odPrintConsoleString(L"\nTurns = %g", pHelix->turns());

To set the turns property, use the setTurns() method which requires a positive double value as an argument and does not return a value. For example:


pHelix->setTurns(4.0);

Note: The specified value must be positive.

Turn Twist

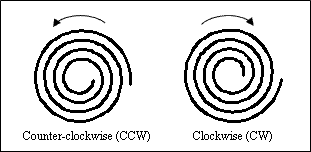
The Turn Twist property defines the direction of turns (counterclockwise or clockwise) for the spiral curve as a Boolean value. If the value is True, the turn is twisted counter-clockwise (CCW). If the value is False, the turn is twisted clockwise (CW). The initial value is True (CCW) by default.

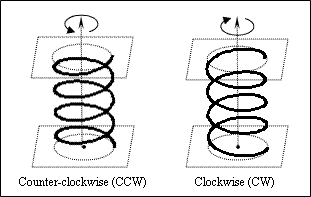
A planar helix also can be twisted counter-clockwise or clockwise from the start point to the end point.

To check the turn twist, use the twist() method which does not have arguments and returns the direction as a Boolean value. For example:


odPrintConsoleString(L"\nHelix is twist %s", ((pHelix->twist()) ? L"CCW" : L"CW"));

To switch the turn twist, use the setTwist() method which requires a Boolean value and does not return a value. For example:


// Set the CCW twist
pHelix->setTwist(true);

// Set the CW twist
pHelix->setTwist(false);

Total Length

The Total Length property defines the length along the spiral curve from the start point to the end point in drawing units. If the total length is zero, the helix transforms into a point. The total length is 1.0 by default.

To get the total length, use the totalLength() method which does not have arguments and returns the length as a double value. For example:


odPrintConsoleString(L"\nTotal length = %g", pHelix->totalLength());

Note: The helix object does not have a method to set the total length; this property is read-only.

Reverse Curve

The reverseCurve() method reverses the helix curve, so that the start point becomes the end point, and vice versa. This method does not have arguments. A first call reverses the curve, and a second call returns it to its original curve. For example:


pHelix->reverseCurve();