Computed Helix Properties

The parameter of a helix is the angle measured from the OCS X-axis in radians. A positive parameter value defines the angle counterclockwise. A negative parameter value defines the angle clockwise. A zero value coincides with the OCS X-axis. A parameter can be changed in the range from 0 to 2PI*turns. The parameter determines the significant properties computed at its value (features). In the following examples, the pHelix variable stores a pointer to the helix object.

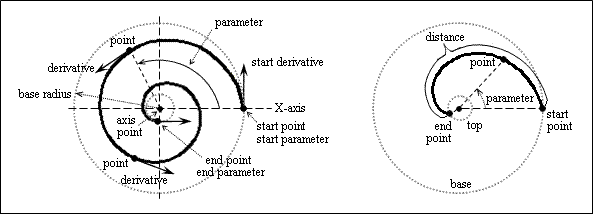
Start and End Parameters

The Start and End parameters of a helix define the available range of its variation. The start parameter equals 0.0 and defines the start point. The end parameter equals 2*PI*turns and defines the end point. A value between the start and end parameters defines a point on the spiral curve.

To get the start parameter, use the getStartParam() method which requires a reference to a variable of the Double type in which the start parameter value must be saved as an argument and returns the start value through this argument or an error code as a result. For example:


double vStartParam;
OdResult eRes = pHelix->getStartParam(vStartParam);
if(eRes == eOk)
  OdConsoleString(L"\nStart parameter = %g", vStartParam);

To get the end parameter, use the getEndParam() method which requires a reference to a variable of the Double type in which the end parameter value must be saved as an argument and returns the end value through this argument or an error code as a result. For example:


double vEndParam;
OdResult eRes = pHelix->getEndParam(vEndParam);
if(eRes == eOk)
  OdConsoleString(L"\nEnd parameter = %g", vEndParam);

Start and End Points

The start and end points are computed at a parameter in three-dimensional coordinates. The start point is computed at the start parameter. The end point is computed at the end parameter. When the helix is planar and the number of turns is an integer, the start point coincides with the end point. The axis point influences the start and end point; the base radius influences the start point; and the top radius influences the end point.

To get the start point, use the getStartPoint() method which requires a reference to a variable of the OdGePoint3d type in which the start point instance must be saved as an argument and returns the computed three-dimensional point through this argument or an error code as a result. For example:


OdGePoint3d start;
OdResult eRes = pHelix->getStartPoint(start);
if(eRes == eOk)
  OdConsoleString(L"\nStart point = (%g,%g,%g)", start.x, start.y, start.z);

To get the end point, use the getEndPoint() method which requires a reference to a variable of the OdGePoint3d type in which the end point instance must be saved as an argument and returns the computed three-dimensional point through this argument or an error code as a result. For example:


OdGePoint3d end;
OdResult eRes = pHelix->getEndPoint(end);
if(eRes == eOk)
  OdConsoleString(L"\nEnd point = (%g,%g,%g)", end.x, end.y, end.z);

Note: The setStartPoint() method sets the start point. The setAxisPoint() method can move the start point and end point.

First and Second Derivatives

The first and second derivatives for a point of a spiral curve are computed at a parameter as vectors in three-dimensional coordinates. Derivatives are changed along the spiral curve. The parameter must be between the start and end values. When the parameter value is out of range, errors occur.

To get the first derivative, use the getFirstDeriv() method which requires a parameter value specifying a point on the spiral curve as the first argument of the Double type, requires a reference to a variable of the OdGeVector3d type in which the first derivative vector instance must be saved as the second argument, and returns the computed three-dimensional vector through the second argument or an error code as a result. For example:


OdGeVector3d vecFirst;
OdResult eRes = pHelix->getFirstDeriv((vEndParam + vStartParam)/2, vecFirst);
if(eRes == eOk)
  OdConsoleString(L"\nFirst derivative vector = (%g,%g,%g)", vecFirst.x, vecFirst.y, vecFirst.z);

To get the second derivative, use the getSecondDeriv() method which requires a parameter value specifying a point on the spiral curve as the first argument of the Double type, requires a reference to a variable of the OdGeVector3d type in which the second derivative vector instance must be saved as the second argument, and returns the computed three-dimensional vector through the second argument or an error code as a result. For example:


OdGeVector3d vecSecond;
OdResult eRes = pHelix->getSecondDeriv((vEndParam + vStartParam)/2, vecSecond);
if(eRes == eOk)
  OdConsoleString(L"\nSecond derivative vector = (%g,%g,%g)", vecSecond.x, vecSecond.y, vecSecond.z);

Distance and Parameter

The distance along a spiral curve can be computed from the start point to a point at a parameter in drawing units. The helix object allows calculating the distance at a parameter and the parameter at a distance.

To get the distance using a parameter, use the getDistAtParam() method which requires a parameter value specifying a point on the spiral curve as the first argument of the Double type, requires a reference to a variable of the Double type in which the distance value must be saved as the second argument, and returns the distance through the second argument or an error code as a result. The parameter must be between the start and end values, otherwise errors occur. For example:


double vTurnLength;
OdResult eRes = pHelix->getDistAtParam(Oda2PI, vTurnLength);
if(eRes == eOk)
  OdConsoleString(L"\nTurn length = %g", vTurnLength);

To compute the total length, use the end parameter value, or alternatively use the totalLength() method. For example:


double vHelixLength;
OdResult eRes = pHelix->getDistAtParam(vEndParam, vHelixLength);
if(eRes == eOk)
  OdConsoleString(L"\nTotal length = %g", vHelixLength);

To get the parameter using a distance, use the getParamAtDist() method which requires a positive double value specifying the displacement along the spiral curve as the first argument of the Double type, requires a reference to a variable of the Double type in which the parameter value must be saved as the second argument, and returns the parameter value corresponding to the distance through the second argument or an error code as a result. The distance must be between zero and the total length, otherwise errors occur. For example:


double vTurnParam;
OdResult eRes = pHelix->getParamAtDist(pHelix->totalLength()/pHelix->turns(), vTurnParam);
if(eRes == eOk)
  OdConsoleString(L"\nTurn parameter = %g", vTurnParam);

Point and Parameter

The point on a spiral curve can be computed at a parameter in three-dimensional coordinates. The helix object allows calculating the point at a parameter and the parameter at point.

To get the point using a parameter, use the getPointAtParam() method which requires a parameter value specifying the point on the spiral curve as the first argument of the Double type, requires a reference to a variable of the OdGePoint3d type in which the point instance must be saved as the second argument, and returns the computed three-dimensional point through the second argument or an error code as a result. When the parameter value is out of range, errors occur. For example:


OdGePoint3d middle;
OdResult eRes = pHelix->getPointAtParam((vEndParam + vStartParam)/2, middle);
if(eRes == eOk)
  OdConsoleString(L"\nMiddle point = (%g,%g,%g)", middle.x, middle.y, middle.z);

To get the parameter using a point, use the getParamAtPoint() method which requires a point instance of the OdGePoint3d type as the first argument, a reference to a variable of the Double type in which the parameter value must be saved as the second argument, and returns the parameter corresponding to the point through the second argument or an error code as a result. When the point is not placed on the spiral curve, errors occur. For example:


double vParam;
OdResult eRes = pHelix->getParamAtPoint(middle, vParam);
if(eRes == eOk)
  OdConsoleString(L"\nParameter = %g", vParam);

Area

The helix object approximates the spiral curve as a spline whose area is calculated. To get the area, use the getArea() method which requires a reference to a variable of the Double type in which the area value must be saved as an argument and returns the area value through this argument or an error code as a result. For example: