Specific Ellipse Properties

The ellipse object uses the center, major axis, minor axis, normal, and radius ratio properties to define the geometry to be drawn. In examples, the pEllipse variable stores the pointer to the ellipse object.

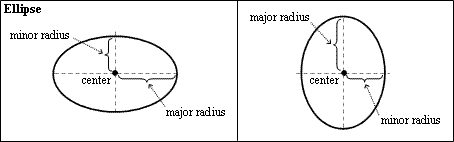
Center

The Center property defines the center of the ellipse in three-dimensional coordinates. The center has the coordinates (0,0,0) by default.

To get the center, use the center() method which does not have arguments and returns the three-dimensional point as an instance of the OdGePoint3d type. For example:


OdGePoint3d center = pEllipse->center();
odPrintConsoleString(L"\nCenter = (%g,%g,%g)", center.x, center.y, center.z);

To set the center, use the setCenter() method which requires the three-dimensional point as an argument of the OdGePoint3d type and does not return a value. For example:


OdGePoint3d point(3.4, 2.3, 1.2);
pEllipse->setCenter(point);

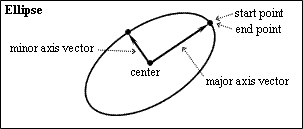
Major and Minor Axises

The Major and Minor Axis properties define the major and minor axes of the ellipse as two perpendicular vectors in three-dimensional coordinates. Major and minor vectors lie in the same plane and the minor vector is not longer than the major vector. Both vectors are coordinated from the center coordinate (0,0,0) and the coordinates of the vectors are not recalculated when the center of the ellipse changes. The major axis vector defines the start and end point for the ellipse. The major axis vector has the coordinates (1,0,0) by default. The minor axis vector has the coordinates (0,1,0) by default.

To get the major axis, use the majorAxis() method which does not have arguments and returns the three-dimensional major vector as an instance of the OdGeVector3d type. For example:


OdGeVector3d majorAxis = pEllipse->majorAxis();
odPrintConsoleString(L"\nMajor Axis = (%g,%g,%g)", majorAxis.x, majorAxis.y, majorAxis.z);

To get the minor axis, use the minorAxis() method which does not have arguments and returns the three-dimensional minor vector as an instance of the OdGeVector3d type. For example:


OdGeVector3d minorAxis = pEllipse->minorAxis();
odPrintConsoleString(L"\nMinor Axis = (%g,%g,%g)", minorAxis.x, minorAxis.y, minorAxis.z);

Note: The ellipse object uses the major axis as a general vector for defining the geometry and recalculates the minor axis using the radius ratio. Only the major axis vector can be specified for the ellipse object.

Major and Minor Radiuses

The property defines the major and minor radiuses of the ellipse as lengths of the major and minor vectors appropriately. Radiuses are positive Double values in drawing units. The major and minor radiuses are equal to 1.0 by default.

To get the major radius, use the length() method of the major axis vector obtained by the majorAxis() method. To get the minor radius, use the length() method of the minor axis vector obtained by the minorAxis() method. For example:


double majorRadius = pEllipse->majorAxis().length();
double minorRadius = pEllipse->minorAxis().length();
odPrintConsoleString(L"\nMajor radius = %g, Minor radius = %g", majorRadius, minorRadius);

Note: The minor radius is less than or equal to the major radius.

Radius Ratio

The property defines the ratio of the minor radius (length of the minor vector) to the major radius (length of the major vector) as a positive Double value. The radius ratio must be in the range of 0.000001 to 1.000000 (minor radius less than major radius). The radius is one by default.

To get the radius ratio, use the radiusRatio() method which does not have arguments and returns the radius ratio as a positive Double value. For example:


odPrintConsoleString(L"\nRadius ratio = %g", pEllipse->radiusRatio());

To set the radius ratio, use the setRadiusRatio() method which requires a positive Double value in the range [1e-6....1] as an argument and does not return a value. For example:


pEllipse->setRadius(0.75);

Note: The ellipse object automatically recalculates the minor axis and minor radius using the major axis and radius ratio.

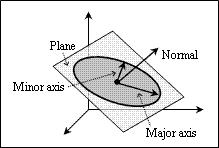
Normal

The Normal property defines the normal to the plane in which the ellipse is placed. The normal defines the orientation of the ellipse in world space. The normal must be perpendicular to the major axis vector. The normal has the coordinates (0,0,1) by default.

To get the normal, use the normal() method which does not have arguments and returns the three-dimensional vector as an instance of the OdGeVector3d type. For example:


OdGeVector3d normal = pEllipse->normal();
odPrintConsoleString(L"\nNormal = (%g,%g,%g)", normal.x, normal.y, normal.z);

Note: If the normal and major axis are not perpendicular, an error occurs.

Setting the Center, Major Axis, Normal, and Radius Ratio

To set the ellipse definition geometry, use the set() method which requires four arguments for a closed ellipse — three-dimensional point instance specifying the center as the first argument of the OdGePoint3d type, three-dimensional unit vector instance specifying the normal as the second argument of the OdGeVector3d type, three-dimensional vector instance specifying the major axis perpendicular to the normal as the third argument of the OdGeVector3d type, and radius ratio in the range [1e-6 to1.0] as the fourth argument of the Double type — and sets the specified properties of the ellipse object. For example: